スクリーニング計画
工程内の最も重要な因子を特定するためによく使用される計画実験です。スクリーニング計画では、数多くの潜在因子と相対的に少ない数の実行を使用して、工程の品質に影響を与える少数の最重要な因子を決定します。スクリーニング実験後、詳細が必要な場合は実験を最適化できます。たとえば、脂肪含有率、低温殺菌時の温度、均質化の工程、混合速度、絞り出し時の温度、乳化剤、安定剤、冷却速度など、ソフトクリームの舌触りに関するさまざまな因子を調べているとします。スクリーニング計画を使用して、ソフトクリームの舌触りに影響を与える最も重要な因子を特定できます。必要があれば、より大きな要因計画または応答曲面計画を使用して工程を最適化できます。
- 決定的スクリーニング計画
- 決定的スクリーニング計画は、二乗項と線形項を推定できるように連続因子ごとに3つの水準が含まれているスクリーニング計画です。線形項は2因子交互作用の別名ではないので、決定的スクリーニング計画により、潜在的に重要な交互作用の根拠を見つけることもできます。たとえば、8つの因子があれば、決定的スクリーニング計画では、3つ以下の重要な因子に対して、線形、二乗、二元交互作用をすべて効率的に適合できます。
- プラケットーバーマン計画
-
プラケットーバーマン計画は、通常、分解能IIIで2水準の計画です。分解能IIIの計画では、主効果は二元交互作用と別名関係にあります。そのため、二元交互作用が無視できる大きさだと仮定できる場合にのみ、この計画を使うようにしてください。この仮説により、プラケットーバーマン計画は決定的スクリーニング計画よりも実行数を少なくできます。プラケットーバーマン計画を実行後、交互作用が存在すると思われる場合、計画を折り重ねて実行数を倍にできます。プラケットーバーマン計画を折り重ねた後、主効果は二元交互作用と別名の関係にはなりません。詳細は、折り重ねとはを参照してください。
要因計画
- 2水準要因計画(既定のジェネレータ)
- 完全実施要因計画または一部実施要因計画を作成するには、このオプションを選択します。既定のジェネレータは、因子数および実行数に対して分解能が最も高い計画を作成します。
- 2水準要因計画(ジェネレータの指定)
- 一部実施要因計画に含める実行のサブセットを指定するために、独自のジェネレータを使用できます。また、項に対してジェネレータを指定することにより、因子を追加したりブロックを定義することもできます。
- 2水準分割実験(変更が難しい因子)
- 変更が難しい因子を少なくとも1つ含む計画実験です。変更が難しい因子とは、時間や費用の制約があるために完全にランダム化するのが困難な因子です。
- プラケット-バーマン計画
-
プラケットーバーマン計画は、通常、分解能IIIで2水準の計画です。分解能IIIの計画では、主効果は二元交互作用と別名関係にあります。そのため、二元交互作用が無視できる大きさだと仮定できる場合にのみ、この計画を使うようにしてください。
Plackett-Burman計画は、実験の初期段階で最も重要な因子を特定するために使用されます。たとえば、脂肪含有率、低温殺菌時の温度、均質化の工程、混合速度、絞り出し時の温度、乳化剤、安定剤、冷却速度など、ソフトクリームの舌触りに関するさまざまな因子を調べているとします。Plackett-Burman計画を使用して最も重要な主効果を特定し、特定された主効果は、一部実施要因計画や完全実施要因計画でさらに調べることができます。その後、応答曲面計画を使用して工程を最適化できます。
- 一般完全実施要因計画
- 因子に任意の数の水準を使用できる計画実験です。因子はすべてカテゴリ因子です。
応答曲面計画
- 中心複合
- 2水準要因計画に中心点と軸点を追加して、曲面性をモデル化する実験計画です。
- Box-Behnken
- ボックスーベンケン計画による実験計画は一般に実験点が少なく、同じ因子数で比べた場合に中心複合計画よりも少ないコストで実施できます。この計画では、1次と2次の係数を効果的に推定できますが、要因計画の実験点を含めることができません。ボックスーベンケン計画には、最大5つの水準を持つ中心複合計画とは異なり、因子ごとに3つの水準が必ずあります。同様に、中心複合計画と異なり、ボックスーベンケン計画には、すべての行の設定など、すべての要因の設定が極端になる実行は絶対に含まれません。
混合計画
混合実験は応答曲面実験の1形態で、調査の対象となる製品が複数の成分または原料で構成されているのが特徴です。産業界での製品設計や製品開発では、混合や配合が行われることが多いため、混合実験が役に立ちます。混合や配合を行うとき、応答は使用する原料成分の比率の関数になります。たとえば、小麦粉、ベーキングパウダー、牛乳、卵、食用油からホットケーキミックスを開発するかもしれません。あるいは、4種類の化学原料を配合して殺虫剤を開発するかもしれません。混合計画に関する詳細は、を参照してください 混合計画とは。
最も簡単な混合実験では、応答(何らかの基準に従って測定した製品の品質または性能)は成分(原料)の相対比率によって決まります。重量や体積などの単位で表した成分の量は、合計すると一定の量になります。要因計画では、これと対照的に応答が各因子の量に応じて変化します。
| 追補していない例 | 追補した例 | |
| 単体重心 |
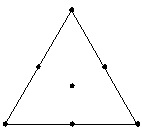 特殊3次モデルまでの適合が可能です。 |
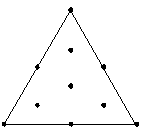 完全3次モデルまでの部分的な適合が可能です。 |
| 単体格子1次 |
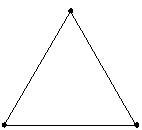 線形モデルの適合が可能です。 |
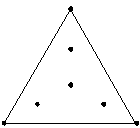 2次モデルまでの部分的な適合が可能です。 |
| 単体格子2次 |
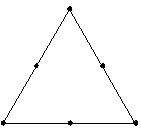 2次モデルまでの適合が可能です。 |
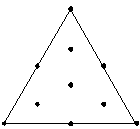 特殊3次モデルまでの部分的な適合が可能です。 |
| 単体格子3次 |
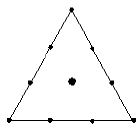 完全3次モデルまでの適合が可能です。 |
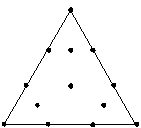 完全3次モデルまでの適合が可能です。 |
- 単体重心
- 計画点がL単体上で一様(格子状)に配置される混合計画です。単体重心計画では、成分数と同じ次数までの項を推定できます。より小さい計画には、推定する項が低次に制限される単体格子計画を使用できます。

この単体重心計画では特殊3次モデルまで推定できます。
- 単体格子
- 計画点がL単体上で一様(格子状)に配置される混合計画です。格子の次数によって適合できる項の次数が決まります。

1次格子は、単体重心計画よりも実行数が少なくなりますが、推定できるのは単純なモデルのみです。

1次格子は、単体重心計画よりも実行数が多くなるため、より複雑なモデルを推定できます。
- 極頂点
-
単体内の一部(より小さい空間)のみを対象とする混合計画です。
極頂点計画の目的は、計画空間を適切に網羅する計画点を選び出すことにあります。次の図は、3つの成分からなる2つの計画に上限制約と下限制約がある場合の極頂点を示しています。
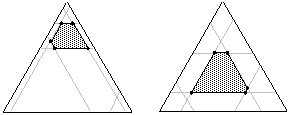
薄い灰色の線は成分の下限制約と上限制約を表します。濃い灰色の領域は計画空間を表します。各点は計画空間の極頂点に配置されます。
タグチ計画
タグチの計画は、動作環境の中で一貫して機能するような製品や工程を選べるように計画された実験です。タグチ計画では、変動を生じさせるすべての因子を制御することは不可能であることを認識しています。これらの制御できない因子は、雑音因子と呼ばれます。タグチ計画では、雑音因子の影響を最小限に抑える制御可能な因子(制御因子)の特定を試みます。実験中、雑音因子を操作して変動性を強制的に生じさせ、工程または製品をロバストにする、つまり雑音因子による変動の影響を受けにくくする最適制御因子を見つけます。この目的のため計画された工程では、より一貫した出力が得られます。また、このような目標に合わせて設計された製品は、製品を使用する環境が変化しても性能が安定しています。
タグチ計画の有名な例は、1950年代に日本の伊奈製陶が実施したものです。当時の伊奈製陶では、製造したタイルが規定寸法外になることがあまりにも多くありました。品質チームは、タイルの焼窯内部の温度が変動する結果、タイルの寸法が不均一になることを突き止めました。窯を新設するには費用がかかりすぎるため、温度の変動を解消することはできませんでした。そのため、温度は雑音因子でした。チームは、タグチ計画の実験を実施して、制御因子である粘土の石灰成分を増やすことにより、窯の温度変動に対するタイルの耐性が増す、つまりロバストになることを発見し、こうしてより均一なタイルを製造できるようになりました。
- 2水準計画
- 各制御因子に2つの水準のみがある計画実験
- 3水準計画
- 各制御因子に必ず3つの水準がある計画実験
- 4水準計画
- 各制御因子に必ず4つの水準がある計画実験
- 5水準計画
- 各制御因子に必ず5つの水準がある計画実験
- 混合水準計画
- 制御因子に異なる数の水準がある計画実験
