このトピックの内容
計画行列
Minitabでは、まず因子と指定したモデルから計画行列が作成されます。この行列の列は、モデルに含まれる項を表しています。作成後、一定の項の列、ブロック、高次項が追加され、分析のモデルに対して計画行列を作成します。
すべての連続因子を持つ計画
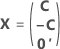
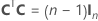
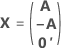
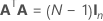
完全計画行列には、因子を表す列のそばに列があります。計画行列には、一定の項に対して値が1の列が含まれます。完全計画行列には、モデル内の二乗項または交互作用項を表す列も含まれます。
カテゴリ因子を持つ計画
計画にカテゴリ因子が含まれている場合、計画行列にある1つの中心点の行は2つの疑似中心点に置き換えられます。計画にカテゴリ因子が1つしかない場合、2つの疑似中心点が存在しうるので、両方のデータ点が計画内にあります。
計画に3つ以上のカテゴリ因子がある場合、反復アルゴリズムを使用して、含まれている2つの疑似中心点を選択します。このアルゴリズムは、モデルに含まれる線形効果の回帰係数の分散が最小化されるように反復します。
表記
| 用語 | 説明 |
|---|---|
| C | カンファレンス行列 |
| 0' | 中心点における実行を表す、行列内のゼロの行 |
| In | n × nの恒等行列 |
| A | 次のような、N行とn列を持つカンファレンス行列のサブセットにあたる行列 |
| N | カンファレンス行列の列のサブセット内にある行の数 |
| n | 計画に含まれる因子の数 |
係数(Coef)
行列項において、モデル内の係数のベクトルを計算する計算式は以下です。

表記
| 用語 | 説明 |
|---|---|
| X | 計画行列 |
| Y | 応答ベクトル |
ボックスーコックス変換
ボックスーコックス変換では、以下に示す通り、二乗値の残差合計を最小化するλ値が選択されます。出力される変換は、λ ≠ 0の場合にYλ、およびλ = 0の場合にln(Y)です。λ < 0の場合に、変換済み応答に−1を掛けて、変換されていない応答の順序を維持します。
−2~2の範囲で最適値が検索されます。値がこの区間外になった場合、適合性が低下することがあります。
以下は一般的な変換方法です(Y′はデータYの変換データ)。
| ラムダ(λ)値 | 変換 |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0.5 | Y′ = 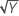 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0.5 |  |
| λ = −1 | Y′ = −1 / Y |
重み付き回帰
重み付き最小二乗回帰は、観測値の分散が不均一な場合に用いられる手法です。分散が一定でない場合、
- 観測値の分散が大きい場合は比較的小さい重みが与えられます
- 観測値の分散が小さい場合は比較的大きい重みが与えられます
通常の重みの選択は、応答の純誤差分散の逆数です。
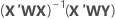
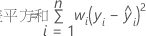
表記
| 用語 | 説明 |
|---|---|
| X | 計画行列 |
| X' | 計画行列の転置 |
| W | 対角線に重みを配置したn×n行列 |
| Y | 応答値のベクトル |
| n | 観測値数 |
| wi | i番目の観測値の重み値 |
| yi | i番目の観測値の応答値 |
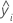 | i番目の観測値の適合値 |
