決定的スクリーニング計画の2値応答を分析の方法

古典的線形モデルの一般化線形モデルへの拡張には2つのパートがあります。指数族の分布とリンク関数です。

指数族

1つ目のパートは、線型モデルを「指数族」と呼ばれる大きな分布族の一部である応答変数に拡張することです。指数分布族の一部には、以下のような一般形で観測された応答の確率分布関数があります。

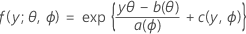
上記の式では、a(∙)、b(∙)、c(∙)は応答変数の分布によって変化します。パラメータθは、しばしば「正準パラメータ」と呼ばれる位置母数パラメータのことを指し、ϕは分散パラメータと呼ばれます。通常、関数a(ϕ)はa(ϕ)= ϕ/ ωという式が成立します（Minitabでは、重みが関数a(ϕ)に設定されている場合はこれに合わせて調整を行います）。

指数族の一部は、離散分布または連続分布になることがあります。指数族の一部となる連続分布の例として、正規分布やガンマ分布があります。指数族の一部となる離散分布の例には、二項分布とポアソン分布があります。以下の表には、このうち幾つかの分布の特徴を記載しています。

分布	ϕ	b(θ)	a(φ)	c(y, ϕ)
正規	σ2	θ2/2	φω
二項	1		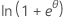φ/ω	-ln(y!)
ポアソン	1	exp(θ)	φ/ω

リンク関数

2つ目のパートはリンク関数です。リンク関数は、i番目の観測値の平均応答を以下の線形予測変数の式に関連付けます。

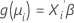
古典的線型モデルは、リンク関数が恒等関数になるような一般的な形式化の特殊ケースです。

2つ目のパートにおけるリンク関数の選択は、1つ目のパートの指数族の特定の分布によって変わります。特に、指数族の各分布には「正準リンク関数」と呼ばれる特殊なリンク関数があります。このリンク関数はg (μ_i) = X_i'β= θという方程式を満たし、θが正準パラメータにあたります。正準リンク関数により、このモデルの望ましい統計的性質が得られます。異なるリンク関数の適合度を比較するには、適合度の統計量を使うことができます。それまでの経緯や各分野での特殊な意味合いに応じ、使われるリンク関数は異なります。たとえば、logitリンク関数の利点の1つは、オッズ比の推定値が得られるという点です。別な例を挙げると、normitリンク関数は、2値カテゴリに分分類される正規分布に従った、基礎変数があると仮定します。

Minitabでは3種類のリンク関数が用意されています。異なるリンク関数により、より幅の広いデータに十分に適合するモデルを見つけることができます。リンク関数はlogit、normit（probitとも呼ばれる)、gompit（相補的log-logとも呼ばれる）です。これらは、標準累積ロジスティック分布関数の逆関数（logit）、標準累積正規分布関数の逆関数（normit）、ゴンペルツ分布関数の逆関数（gompit）です。logitは二項モデルの正準リンク関数であるため、logitはデフォルトのリンク関数です。

モデル	名前	リンク関数、g(μi)
二項	logit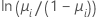
二項	normit（probit）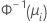
二項	gompit（相補的log-log）

表記

用語	説明
μi	i行目の平均応答
g(μi)	リンク関数
X	予測変数のベクトル
β	予測変数に関連する係数のベクトル
	正規分布の逆累積分布関数

データセット内の1組の因子/共変量の値を説明します。因子/共変量パターンごとに、事象確率、残差、およびその他の診断測定値が計算されます。

たとえば、データセットに性別や人種の因子、年代の共変量が含まれている場合、これらの予測変数の組み合わせには、統計対象と同じ数のさまざまな共変量パターンが含まれている可能性があります。データセットに人種や性別の因子のみが含まれ、それぞれ2つの水準でコード化されている場合は、4つの因子/共変量パターンしかありません。データを、頻度または成功、試行、もしくは失敗として入力する場合、各行には1つの因子/共変量パターンが含まれます。

Minitabでは、まず因子と指定したモデルから計画行列が作成されます。この行列の列は、モデルに含まれる項を表しています。作成後、一定の項の列、ブロック、高次項が追加され、分析のモデルに対して計画行列を作成します。

すべての連続因子を持つ計画

計画行列の形式は、因子と同じ行数でカンファレンス行列が存在するかどうかによって変わります。この基準が真のとき、因子を表す計画行列の列には以下の形式があります。

Cは要素{-1, 0, 1}を持つn × nのカンファレンス行列であり、次の特性を満たします。

正しいサイズのカンファレンス行列が存在しないとき、因子を表す列は、より大きなカンファレンス行列のサブセットです。

Cは要素{-1, 0, 1}を持つn × nの行列であり、次の特性を満たします。

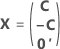
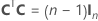
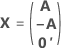
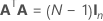
完全計画行列には、因子を表す列のそばに列があります。計画行列には、一定の項に対して値が1の列が含まれます。完全計画行列には、モデル内の二乗項または交互作用項を表す列も含まれます。

カテゴリ因子を持つ計画

計画にカテゴリ因子が含まれている場合、計画行列にある1つの中心点の行は2つの疑似中心点に置き換えられます。計画にカテゴリ因子が1つしかない場合、2つの疑似中心点が存在しうるので、両方のデータ点が計画内にあります。

計画に3つ以上のカテゴリ因子がある場合、反復アルゴリズムを使用して、含まれている2つの疑似中心点を選択します。このアルゴリズムは、モデルに含まれる線形効果の回帰係数の分散が最小化されるように反復します。

表記

用語	説明
C	カンファレンス行列
0'	中心点における実行を表す、行列内のゼロの行
In	n × nの恒等行列
A	次のような、N行とn列を持つカンファレンス行列のサブセットにあたる行列
N	カンファレンス行列の列のサブセット内にある行の数
n	計画に含まれる因子の数