決定的スクリーニング計画の2値応答を分析の診断測度の方法と計算式

このトピックの内容

ピアソン残差
標準化ピアソン残差と削除ピアソン残差
逸脱残差
標準化逸脱残差
削除逸脱残差
⊿χ2（デルタカイ二乗）
⊿逸脱度
⊿ベータ（標準化）
⊿ベータ
てこ比
Cookの距離
DFITS
分散拡大係数（VIF: Variance Inflation Factor）

ピアソン残差

不適合な因子・共変量パターンを検出するために使用できるピアソンカイニ乗の要素。Minitabでは、i番目の因子・共変量パターンのピアソン残差を保存します。式は以下になります。

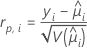
表記

用語	説明
y_i	i番目の因子・共変量パターンの応答値
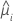	i番目の因子・共編量パターンの適合値
V	におけるモデルの分散関数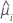

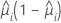
次の式では二項モデルの分散関数が算出されます。

標準化ピアソン残差と削除ピアソン残差

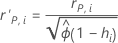
不適合因子・共変量パターンの検出に使用します。Minitabはi番目の因子・共変量パターンの標準化ピアソン残差を保存します。削除ピアソン残差は尤度比ピアソン残差とも呼ばれます。削除ピアソン残差の場合、Minitabはプレジボンの¹で示される1ステップ近似値を計算します。この近似値は標準化ピアソン残差に等しくなります。計算式は以下になります。

表記

用語	説明
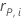	i番目の因子・共変量パターンのピアソン残差
	1（二項モデルの場合）
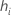	i番目の因子・共編量パターンのてこ比

逸脱残差

逸脱残差はモデル逸脱度を基にしており、不適合の因子/共変量パターンを特定するのに役立ちます。モデル逸脱度は、対数尤度関数に基づいた適合度統計量です。i番目の因子/共変量パターンに対して定義される逸脱残差は以下になります。

表記

用語	説明
y_i	i番目の因子/共変量パターンの応答値
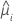	i番目の因子/共編量パターンの適合値
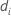	i番目の因子/共編量パターンの逸脱度

標準化逸脱残差

標準化逸脱残差は外れ値の特定に役立ちます。計算式は以下になります。

表記

用語	説明
r_D,i	i番目の因子/共編量パターンの逸脱残差
h_i	i番目の因子/共編量パターンのてこ比

削除逸脱残差

削除された逸脱残差は、データからのi番目の省略による逸脱の変更を測定します。削除された逸脱残差は尤度比逸脱残差とも呼ばれます。削除された逸脱残差については、Minitabではプレジボン1段階近似法¹に基づいて、1段階近似が計算されます。計算式は次のとおりです。

表記

用語	説明
y_i	i番目にある因子/共変量パターンの応答値
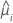	i番目の因子共編量パターンの適合値
h_i	i番目の因子/共編量パターンのてこ比
r'_D,i	i番目の因子/共変量パターンの標準化された逸脱残差
r'_P,i	i番目の因子/共変量パターンの標準化されたピアソン残差

1. Pregibon, D. (1981). "Logistic Regression Diagnostics." The Annals of Statistics, Vol. 9, No. 4 pp. 705–724.

⊿χ2（デルタカイ二乗）

j番目の因子/共変量パターンを持つすべての観測値を削除することによる、ピアソンカイ二乗の変化量を計算します。データの異なる因子/共変量パターンごとに1つの⊿χ2（デルタカイ二乗）値が保存されます。⊿χ2を使用して、不適合な因子/共変量パターンを検出できます。⊿χ2の計算式は以下になります。

計算式

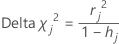
表記

用語	説明
h_j	てこ比
r_j	ピアソン残差

⊿逸脱度

Minitabでは、j番目の因子/共変量パターンの全ての観測値を削除することにより、逸脱量の変化を計算します。データ内の異なる因子/共変量パターンごとに1つの値を保存します。不適合因子/共変量パターンの検出に、⊿逸脱度を使用します。逸脱量の変化は以下の通りです。

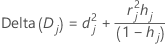
表記

用語	説明
h_j	てこ比
r_j	ピアソン残差
d_j	逸脱残差

⊿ベータ（標準化）

j番目の因子/共変量パターンを持つすべての観測値を削除することで、変化量を計算します。データ内の異なる因子/共変量パターンごとに1つの値が保存されます。標準化された⊿βを使用して、係数の推定値に強い影響を与える因子/共変量パターンを検出できます。この値は、標準化されたピアソン残差に基づいています。

計算式

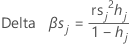
表記

用語	説明
h_j	てこ比
rs _j	標準化されたピアソン残差

⊿ベータ

j番目の因子/共変量パターンを持つすべての観測値を削除することで、変化量を計算します。データ内の異なる因子/共変量パターンごとに1つの値が保存されます。⊿βを使用して、係数の推定値に強い影響を与える因子/共変量パターンを検出できます。この値は、ピアソン残差に基づいています。

計算式

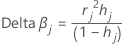
表記

用語	説明
h_j	てこ比
r_j	ピアソン残差

てこ比

てこ比は、一般化されたハット行列の対角要素です。てこ比は、結果に有意な影響を与える可能性のある因子/共編量パターンを検出するのに役立ちます。

計算式

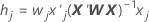
表記

用語	説明
w_j	係数を適合させることにより得られる重み行列のj番目の対角要素
x_j	j行目の計画行列
X	計画行列
X'	Xの転置
W	係数の推定から得られる重み行列

Cookの距離

Minitabでは、Cookの距離の近似値を計算します。

計算式

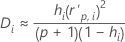
表記

用語	説明
h_i	i番目の因子/共編量パターンのてこ比
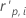	i番目の因子/共変量パターンの標準化されたピアソン残差
p	回帰自由度

DFITS

適合値を削除することによる影響の測定。DFITSの値が大きい観測値は外れ値になることがあります。Minitabでは、DFITSの近似値を計算します。

計算式

表記

用語	説明
h_i	データ点のてこ比
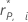	データ点の削除ピアソン残差

分散拡大係数（VIF: Variance Inflation Factor）

VIFを求めるには、予測変数と残りの予測変数の加重回帰を実行します。重み行列はマカラおよびネルダー¹の係数の推定で示される行列です。この場合、VIFの計算式は線形回帰の計算式と同等になります。たとえば、予測変数x_jの場合VIFを求める計算式は次のようになります。

表記

用語	説明
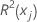	x_jを応答変数、モデル内の他の項を予測変数とする決定係数

1. P. McCullagh and J. A. Nelder (1989年)。 Generalized Linear Models, 2^nd Edition, Chapman & Hall/CRC, London.