決定的スクリーニング計画の2値応答を分析の分散分析の方法と計算式

逸脱度は、現在のモデルと完全モデルの誤差を測定します。完全モデルは、n個のパラメータ（観測値ごとに1つのパラメータ）があるモデルです。完全モデルは対数尤度関数を最大化します。完全モデルは、nよりも少ないパラメータを持つモデルの類似点を導き出します。完全モデルの比較では、スケール逸脱度を使用します。

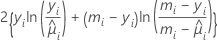
逸脱度表は、ϕが既知であると仮定して導き出される以下の一般的な結果に基づいて解釈されます。D_Iが初期モデルと関連のある逸脱度であり、D_Sが初期モデルのサブセットの項と関連する逸脱度である場合、いくつかの正則条件下では、以下のような関係があります。

逸脱度間の差は、d個の自由度を持つカイ二乗分布として漸近的に分布します。これらの統計量は調整済み（タイプIII）分析と連続（タイプI）分析用に計算されます。調整済み逸脱度と逸脱度表のカイ二乗統計量は等しくなります。調整済み平均逸脱度は、調整済み逸脱度を自由度で除算したものです。

逐次分析の場合、出力結果は、予測変数がモデルに入力される順序によって変わります。逐次逸脱度はモデル内に予測変数が既にあることを前提として、予測変数が説明する逸脱度の固有部です。モデルにX1、X2、X3の3つの予測変数がある場合、X3の逐次逸脱度は、モデル内にX1、X2が既にあることを前提として、これらの残りの逸脱度の値を明らかにします。異なる逐次逸脱度を得るには、異なる順序で予測変数を入力する回帰手法を繰り返します。

ϕが未知である場合、正規分布に基づく応答に関しては、正則条件下で以下のような関係の変化があります。

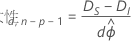
ここでは、逸脱度間の差は、分子にd個の自由度、分母にn − p個の自由度を持つF分布として漸近的に分布します。分散パラメータを推定するには、初期モデルを使用します。

表記

用語	説明
yi	i行目の事象数
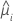	i行目の推定平均応答
mi	i行目の試行数
Lf	完全モデルの対数尤度
Lc	完全モデルのサブセットの項を持つモデルの対数尤度
d	自由度は、比較するモデル内のパラメータ数の差です
ϕ	分散パラメータ（二項モデルでは1として知られている）
n	データの行数
p	初期モデルの回帰自由度

異なる平方和に、異なる自由度があります。

数値因子 = 1の自由度

カテゴリ因子 = b − 1の自由度

2次項 = 1の自由度

ブロック = c − 1の自由度

誤差 = n − pの自由度

自由度の合計 = n − 1

表記

用語	説明
b	因子の水準数
c	ブロック数
n	計画に含まれる総行数
ni	i番目の因子水準の組み合わせの観測値数
m	因子水準の組み合わせ数
p	係数の数

対数尤度関数は、パラメータを平均に換算して表します。関数の一般形は以下になります。

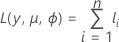
各寄与度の一般形は以下になります。

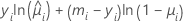
表記

用語	説明
yi	i行目の事象数
mi	i行目の試行数
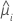	i行目の推定平均応答

p値は、仮説検定で帰無仮説を棄却できるかどうかを決定するために使用されます。p値は帰無仮説が真の場合に、実際の計算値と少なくとも同程度以上の極端な検定統計量が得られる確率です。p値用によく使用されるカットオフ値は0.05です。たとえば、検定統計量の計算されたp値が0.05未満の場合、帰無仮説を棄却します。