因子
数字は、計画内の因子数を示しています。
解釈
因子とは、実験において制御する変数のことを言います。独立変数、説明変数、予測変数とも呼ばれます。因子によって仮定できる有効値の数には限りがあり、因子水準として知られています。因子はテキストまたは数値の水準を持ちます。数値の因子では、可能な因子の値は数多くありますが、実験用の特定の水準を選択します。
たとえば、化学者は水晶の成長を最大化する方法を研究しているとします。化学者は3つの連続変数(時間、温度、室内の空気に含まれる触媒の割合)とカテゴリ因子(加法)を研究したいと考えます。
応答曲面計画では、各連続因子に対し、低水準と高水準を割り当てます。因子水準によって「キューブ」が定義され、計画は「キューブ」の周りに構築されます。「キューブ」は、工程の現在の実施条件を中心とするのが普通です。中心複合計画の場合、「キューブ」の内側、「キューブ」の上、「キューブ」の外側のいずれかに計画点があります。
ベースと実行総数
ベース実行数は、基本計画における因子水準の組み合わせ数です。実行総数は、ベース実行数に反復数を掛けた数です。
解釈
| 実行 | 因子1 | 因子2 | 応答 |
|---|---|---|---|
| 1 | −1 | −1 | 11 |
| 2 | 1 | −1 | 12 |
| 3 | −1 | 1 | 10 |
| 4 | 1 | 1 | 9 |
注
実験を実行する場合は、実行順序をランダム化してください。
各実行は計画点に対応し、実行のセット全体が計画になります。同じ実験条件で行われる複数回の実行は、それぞれ別の実行とみなされ、反復と呼ばれます。
ベースブロックとブロック総数
ブロックは同じ構造を持った実験単位(観測値)の群です。ベースブロックとは、反復を計画に加える前のブロック数です。ブロック総数には、反復によって作成されたブロックが含まれます。
各観測値は(実験の一部として実験条件が変わる場合を除き)同一の実験条件で測定される必要がありますが、それが不可能な場合もあります。分類可能な攪乱因子は、ブロック化された計画により取り除くことができます。たとえば、実験が何日かに分けて実施され、その間に温度と湿度が大きく変動する場合や、データが異なる植物から異なる技官により取得される場合があります。同じ実験条件で収集された観測値は、同じブロックに属すると言います。
反復
数字は、計画内の反復数を示しています。
解釈
反復とは、同じ因子水準設定(水準)で実験を複数回実行することです。1回の反復は、各因子水準の組み合わせを1回実行する基本計画と同等です。反復が2回になると、基本計画の各因子水準の組み合わせを2回(ランダムに)実行、という風に続きます。
たとえば、それぞれ2水準の因子が3つ存在するときに、因子水準の組み合わせすべてを試験する場合(完全実施要因計画)、基本となる計画は1回の反復を表し、8回の実行(23)があります。2回の反復を追加する場合、計画には3回の反復と24回の実行が含まれます。
- 予測モデルを作成する場合は、複数回の反復によってモデルの精度が高まる可能性があります。
- 反復を組み込む場合、小さな効果を検出したり、大きな検出力で固定サイズの効果を検出したりすることが可能になります。
- スクリーニング計画(2水準因子計画)には、大きな因子のセットを減らすために使用するものであり、通常反復は含まれません。
- ご使用のリソースによっては、実行可能な反復数を記述できる場合があります。たとえば、実験に極端な費用がかかる場合に、基本となる計画を一度だけ実行できることもあります。
反復(replicate)と反復(repeat)の違いに関する詳細は、計画実験における反復と繰り返しを参照してください。
アルファ
アルファ(α)により、中心複合計画における各軸点(星点とも呼ばれる)の中心からの距離を決定します。
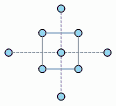
α値が1未満の場合、軸点は立方体の中に位置します。また、α値が1に等しい場合、軸点は立方体の面上、1より大きい場合は、立方体の外に位置します。
アルファおよび中心点の数によって、その計画を直交ブロック化できるかどうか、および回転できるかどうかが決まります。直交ブロック化した計画では、モデル項とブロック効果を別々に推定し、回帰係数の変動性を最小限に抑えることができます。回転が可能な計画では、計画の中心から等距離にあるすべての点で予測分散が一定になります。
計画にブロックが含まれていて、両方の特性を持たせることができないときは、デフォルトで、計画が直交ブロックを含むようになるαが採用されます。ブロックがないときは、デフォルトの計画では、計画が回転可能になるようなαが採用されます。
Minitabのアルファ値は、Montgomery(1)にリスト化された値と一致します。
立方体の点、立方体の中心点、軸点
中心複合計画は、2K要因計画または2k−p一部実施要因計画の計画点により構成される「キューブ(立方体)」部分と2K軸点(または「星」点)および中心点からなります(ここでKは因子数)。
解釈

軸の中心点
すべての因子が同時にそれぞれの中央水準に設定され、軸ブロックにある計画点。軸ブロックは、立方体の点ではなく、軸点が含まれるブロックです。
解釈
- 因子Aは、低水準20および高水準30を持つ
- 因子Bは、低水準150および高水準200を持つ
この計画の中心点は、因子Aが25、因子Bが175にそれぞれ等しい点になります。
計画表
計画表には、実験実行ごとの因子設定が表示されます。計画表はワークシートよりもスペースを取りませんので、制限されたスペースのレポートに役立ちます。
- -1は低因子水準を示します。
- 1は高水準を示します。
- 0は低水準と高水準の中央の点を示します。
- 負と正のデフォルトのアルファ値は、軸上の低水準と高水準をそれぞれ示します。
カテゴリ因子では、カテゴリに対応する数字を持つ因子設定を表します。
解釈
計画表を使用して、実行の因子設定と計画の実行順序を確認します。これらの結果では、計画表には2つのブロックごとに実行数14、合計28の実行数が表示されます。実行はブロックごとにランダム化されます。-1.414と1.414は、軸上の低水準と高水準を示します。最初の実行では、連続因子AとBは最高水準と最低水準の中間点、カテゴリ因子Cは水準1にあります。
計画表 (ランダム化)
| 実行 | Blk | A | B | C |
|---|---|---|---|---|
| 1 | 1 | 0.00000 | 0.00000 | 1 |
| 2 | 1 | -1.00000 | -1.00000 | 1 |
| 3 | 1 | 1.00000 | -1.00000 | 1 |
| 4 | 1 | 0.00000 | 0.00000 | 1 |
| 5 | 1 | -1.00000 | -1.00000 | 2 |
| 6 | 1 | 0.00000 | 0.00000 | 1 |
| 7 | 1 | -1.00000 | 1.00000 | 1 |
| 8 | 1 | 1.00000 | 1.00000 | 2 |
| 9 | 1 | 1.00000 | 1.00000 | 1 |
| 10 | 1 | -1.00000 | 1.00000 | 2 |
| 11 | 1 | 0.00000 | 0.00000 | 2 |
| 12 | 1 | 0.00000 | 0.00000 | 2 |
| 13 | 1 | 0.00000 | 0.00000 | 2 |
| 14 | 1 | 1.00000 | -1.00000 | 2 |
| 15 | 2 | 0.00000 | 0.00000 | 2 |
| 16 | 2 | 0.00000 | 0.00000 | 1 |
| 17 | 2 | 0.00000 | 1.41421 | 2 |
| 18 | 2 | -1.41421 | 0.00000 | 1 |
| 19 | 2 | -1.41421 | 0.00000 | 2 |
| 20 | 2 | 0.00000 | 0.00000 | 2 |
| 21 | 2 | 0.00000 | -1.41421 | 2 |
| 22 | 2 | 0.00000 | 0.00000 | 1 |
| 23 | 2 | 0.00000 | -1.41421 | 1 |
| 24 | 2 | 1.41421 | 0.00000 | 2 |
| 25 | 2 | 0.00000 | 0.00000 | 2 |
| 26 | 2 | 0.00000 | 0.00000 | 1 |
| 27 | 2 | 0.00000 | 1.41421 | 1 |
| 28 | 2 | 1.41421 | 0.00000 | 1 |
