目的の方法または計算式を選択してください。
このトピックの内容
計画行列
計画ごとの計画行列を作成します。最初の列は定数項の列です。計画がK個のブロックにブロック化されている場合は、ブロックが(K-1)列存在します。ブロックのコード化は、要因配置モデルと同じ方法で使用します。その後、各主効果の列が続きます。カテゴリ因子を持つ項は複数列設定できます。モデルに二乗項が含まれる場合は、各二乗項に1列が割り当てられます。二乗項の列は、対応する因子とその二乗項の積になっています。モデルに交互作用項が含まれる場合は、各交互作用項に1列が割り当てられます。カテゴリ因子が含まれている交互作用は複数列設定できます。交互作用項の列は、交差している2つの列の積になっています。
データによってサポートされない項が削除された場合、これらの項は、保存されて計画行列には表示されません。保存される行列の列数は、表示される係数の数と一致します。
係数(Coef)
行列項において、モデル内の係数のベクトルを計算する計算式は以下です。

表記
| 用語 | 説明 |
|---|---|
| X | 計画行列 |
| Y | 応答ベクトル |
ボックスーコックス変換
ボックスーコックス変換では、以下に示す通り、二乗値の残差合計を最小化するλ値が選択されます。出力される変換は、λ ≠ 0の場合にYλ、およびλ = 0の場合にln(Y)です。λ < 0の場合に、変換済み応答に−1を掛けて、変換されていない応答の順序を維持します。
−2~2の範囲で最適値が検索されます。値がこの区間外になった場合、適合性が低下することがあります。
以下は一般的な変換方法です(Y′はデータYの変換データ)。
| ラムダ(λ)値 | 変換 |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0.5 | Y′ = 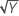 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0.5 |  |
| λ = −1 | Y′ = −1 / Y |
