目的の方法または計算式を選択してください。
適合値
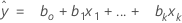
表記
| 用語 | 説明 |
|---|---|
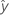 | 適合値 |
| xk | k番目の項。各項は1つの予測変数、多項式の項、または交互作用項になり得ます。 |
| bk | k番目の回帰係数の推定値 |
適合値の標準誤差(SE Fit)
1つの予測変数を持つ回帰モデルにおける適合値の標準誤差:

2つ以上の予測変数を持つ回帰モデルにおける適合値の標準誤差:

重み付け回帰の場合、式に重み行列を含めます。

データにテスト データセットまたは K 折りクロス検証がある場合、数式は同じです。の値 s2はトレーニングデータから。設計マトリックスと重量マトリックスもトレーニングデータから取得されます。
表記
| 用語 | 説明 |
|---|---|
| s1 | mean square error |
| n | number of observations |
| x0 | new value of the predictor |
 | mean of the predictor |
| xii | i番目の predictor value |
| x0 | vector of values that produce the fitted values, one for each column in the design matrix, beginning with a 1 for the constant term |
| x 2」と定義されます。0 | transpose of the new vector of predictor values |
| X | design matrix |
| W | weight matrix |
残差
残差とは、観測値とそれに対応する適合値の差です。観測値のこの部分はモデルでは説明ができません。観測値の残差は以下になります。
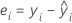
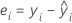
表記
| 用語 | 説明 |
|---|---|
| yi | i番目に観測された応答値 |
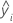 | i番目の応答適合値 |
標準化残差(Std Resid)
標準化残差は、「内部的スチューデント化残差」とも呼ばれます。
計算式

表記
| 用語 | 説明 |
|---|---|
| ei | i番目の残差 |
| hi | X(X'X)–1X'のi番目の対角要素 |
| s2 | 誤差の平均平方 |
| X | 計画行列 |
| X' | 計画行列の転置 |
削除した(スチューデント化)残差
外部でステューデント化された残差とも呼ばれます。計算式は以下になります。
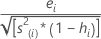
その他の式は以下になります。

i番目の観測値を推定するモデルは、データセットからi番目の観測値を除外します。従ってi番目の観測値は推定値に影響を与えません。削除された各残差には、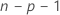 の自由度。
の自由度。
表記
| 用語 | 説明 |
|---|---|
| ei | i番目の残差 |
| s(i)2 | i番目の観測値を使わずに計算された平均平方誤差 |
| hi | X(X'X)–1X'のi番目の対角要素 |
| n | 観測値数 |
| p | 定数項を含む項の数 |
| 残差平方和(SSE) | 誤差の平方和 |
信頼区間
特定の予測値における推定された平均応答値が分類されると予測される範囲。この区間は、信頼水準と適合値の標準誤差から計算される下限と上限によって定義されます。

ここで、

表記
| 用語 | 説明 |
|---|---|
| α | 選択されたα値 |
| n | 観測値数 |
| p | パラメータ数 |
| s2 | 誤差の平均平方 |
| s2{b} | 係数の分散共分散行列 |
予測区間
新しい観測値の予測応答が含まれると予想される範囲。この区間は、信頼水準と予測の標準誤差から計算される下限と上限によって定義されます。平均応答の場合と比較して、単一の応答を予測する際には不確実性が増加するので、予測区間は必ず信頼区間よりも広くなります。
式は以下になります。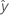 0+ t(1 -α /2; n - p) s(pred)
0+ t(1 -α /2; n - p) s(pred)
表記
| 用語 | 説明 |
|---|---|
| α | 選択されたα値 |
| n | 観測値数 |
| p | 予測変数の数 |
| s (predi | 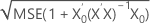 |
