このトピックの内容
ステップ1:応答に対して最大の効果を持つ項を特定する
標準化効果のパレート図は、主効果、二乗効果、交互作用効果について、相対的重要度と統計的有意性の両方を比較するために使用します。
Minitabでは、標準化効果が絶対値の大きなものから小さなものに向かってプロットされます。管理図上の参照ラインは、効果の有意性を示します。参照線の作成には、デフォルトで有意水準0.05が使用されます。
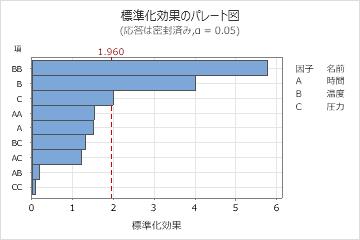
主要な結果:パレート図
これらの結果で、温度(BB)の二乗項、温度(B)と圧力(C)の主効果は、α = 0.05の有意水準において有意です。
また、温度*温度(BB)は最も長く伸びているため、これが最大の効果を持つこともわかります。最も小さい圧力*圧力(CC)が最小です。
ステップ2:応答に対して統計的に有意な効果を持つ項を特定する
モデルにおける応答と各項の間の関係が統計的に有意かどうか判断するには、項のp値と有意水準を比較して帰無仮説を評価します。この帰無仮説は、項の係数は0に等しく、項と応答に関連性がないという仮定です。通常は、有意水準(αまたはアルファとも呼ばれる)として0.05が適切です。0.05の有意水準は、実際には関連性がない場合でも、関連性が存在すると結論付けてしまうリスクが5%であるということを示します。
- p値 ≤ α:関連性は統計的に有意である
- p値が有意水準以下の場合は、応答変数と項の間に統計的に有意な関連性が存在すると結論付けることができます。
- p値 > α:その関連性は統計的に有意ではない
- p値が有意水準より大きい場合は、応答変数と項の間に統計的に有意な関連性があると結論することはできません。項を持たないモデルを再適合したいと考えるかもしれません。
- 因子の係数が有意である場合、事象の確率が全ての因子水準で同じではないと結論付けることができます。
- 二乗項の係数が統計的に有意な場合は、因子と応答の間の関係が曲線になると結論付けることができます。
- 交互作用項の係数が有意な場合は、因子と応答の間の関係はその項の他の因子に依存します。こうしたケースでは、交互作用の影響の考慮なしに主効果を解釈すべきではありません。
- ブロックの係数が統計的に有意である場合、ブロックのリンク関数は平均値と異なると論付けることができます。
コード化係数
| 項 | 係数 | 係数の標準誤差 | VIF |
|---|---|---|---|
| 定数 | 3.021 | 0.384 | |
| 時間 | 0.210 | 0.139 | 18.53 |
| 温度 | 0.641 | 0.159 | 19.53 |
| 圧力 | 0.420 | 0.211 | 70.48 |
| 時間*時間 | -0.0735 | 0.0482 | 1.01 |
| 温度*温度 | 0.2988 | 0.0517 | 1.17 |
| 圧力*圧力 | -0.0022 | 0.0277 | 70.24 |
| 時間*温度 | -0.0092 | 0.0505 | 1.14 |
| 時間*圧力 | 0.0417 | 0.0342 | 18.12 |
| 温度*圧力 | -0.0521 | 0.0396 | 19.24 |
主要な結果:係数
この結果では、時間、温度、圧力の主効果の係数は正の数です。時間*時間の二乗項の係数は負の数です。一般的に、項の値が増加するにつれ、係数が正の場合は事象の可能性は高くなり、係数が負の場合は事象の可能性は低くなります。
分散分析
| 要因 | 自由度 | 調整偏差 | 調整平均 | カイ二乗 | p値 |
|---|---|---|---|---|---|
| モデル | 9 | 903.478 | 100.386 | 903.48 | 0.000 |
| 時間 | 1 | 2.303 | 2.303 | 2.30 | 0.129 |
| 温度 | 1 | 16.388 | 16.388 | 16.39 | 0.000 |
| 圧力 | 1 | 3.966 | 3.966 | 3.97 | 0.046 |
| 時間*時間 | 1 | 2.331 | 2.331 | 2.33 | 0.127 |
| 温度*温度 | 1 | 34.012 | 34.012 | 34.01 | 0.000 |
| 圧力*圧力 | 1 | 0.006 | 0.006 | 0.01 | 0.937 |
| 時間*温度 | 1 | 0.033 | 0.033 | 0.03 | 0.856 |
| 時間*圧力 | 1 | 1.490 | 1.490 | 1.49 | 0.222 |
| 温度*圧力 | 1 | 1.731 | 1.731 | 1.73 | 0.188 |
| 誤差 | 5 | 23.404 | 4.681 | ||
| 合計 | 14 | 926.882 |
主要な結果:p値
これらの結果で、温度*温度の二乗項、温度と圧力の主効果は、α = 0.05の有意水準において有意です。
ステップ3:予測変数の効果を理解する
- 連続予測変数のオッズ比
-
オッズ比が1より大きい場合、予測変数が増加するにつれて事象が発生する可能性が高くなることを示しています。オッズ比が1未満の場合、予測変数が増加するにつれて事象が発生する可能性が低くなることを示しています。
連続予測変数のオッズ比
変更ユニット オッズ比 95%信頼区間 投薬量(mg) 0.5 6.1279 (1.7218, 21.8087) 主要な結果:オッズ比
これらの結果では、モデルは薬の投与水準を使用して、成人の体内のバクテリアの有無を予測します。この例ではバクテリアがないことが事象に該当します。各錠剤に0.5mgの投与量があるので、研究者は0.5mgの単位変化を使用します。オッズ比はおよそ6です。成人が服用する錠剤を追加する度に、患者にバクテリアがないというオッズは約6倍増加します。
- カテゴリ予測変数のオッズ比
-
カテゴリ変数の場合、オッズ比は、予測変数の2つの異なる水準に出現する事象のオッズを比較します。水準Aと水準Bの2つの列に水準を登録することによって比較を設定できます。水準Bは因子の参照水準です。オッズ比が1より大きい場合、事象は水準Aになる可能性が高くなることを示します。オッズ比が1未満の場合、事象は水準Aになる可能性が低くなることを示します。カテゴリ予測変数のコーディングに関する詳細はカテゴリ予測変数のコード化方式を参照してください。
カテゴリ予測変数のオッズ比
水準A 水準B オッズ比 95%信頼区間 月 2 1 1.1250 (0.0600, 21.0834) 3 1 3.3750 (0.2897, 39.3165) 4 1 7.7143 (0.7461, 79.7592) 5 1 2.2500 (0.1107, 45.7172) 6 1 6.0000 (0.5322, 67.6397) 3 2 3.0000 (0.2547, 35.3325) 4 2 6.8571 (0.6556, 71.7169) 5 2 2.0000 (0.0976, 41.0019) 6 2 5.3333 (0.4679, 60.7946) 4 3 2.2857 (0.4103, 12.7323) 5 3 0.6667 (0.0514, 8.6389) 6 3 1.7778 (0.2842, 11.1200) 5 4 0.2917 (0.0252, 3.3719) 6 4 0.7778 (0.1464, 4.1326) 6 5 2.6667 (0.2124, 33.4861) 主要な結果:オッズ比
この結果では、カテゴリ予測変数はホテルの繁忙期の開始月です。応答は、宿泊客が予約をキャンセルするかどうかです。この例ではキャンセルは事象です。最大オッズ比は7.71で、水準Aが4か月目のときと水準Bが1か月目のときが当てはまります。これは、宿泊客が4か月目に予約をキャンセルするオッズは、宿泊客が1か月目に予約をキャンセルするオッズよりも約8倍高いことを示しています。
ステップ4:データに対するモデルの適合度を判断する
注
モデル要約統計量や適合度統計量の多くは、ワークシート内のデータの配置や各行で試行が1回なのか複数回なのかによって影響されます。ホスマー-レメショウ検定は、データの配置に影響されず、行ごとで1回の試行の場合と複数の試行の場合とで比較されます。詳細はデータフォーマットが2値ロジスティック回帰の適合値に与える影響を参照してください。
- 逸脱度R二乗
-
逸脱R2値が大きくなるほど、データへのモデル適合度は上がります。逸脱R2は必ず0~100%の間の値になります。
逸脱度R2はモデルに新しい項を追加すると必ず大きくなります。たとえば、最適な5項モデルのR2は必ず、最適な4項モデルと少なくとも同じ大きさになります。したがって、逸脱度R2値は同じ大きさのモデルの比較に最も便利です。
データの配置は逸脱度R2値に影響します。逸脱度R2は通常、行ごとに試行が1回の場合のデータより複数の試行の場合のデータの方が高くなります。逸脱度R2値は同じデータフォーマットのモデル間でのみ比較可能です。
適合度統計量は、データに対するモデルの適合度を測る1つの測度に過ぎません。モデルの値が望ましい場合でも残差プロットと適合度検定を確認してデータに対するモデルの適合度を評価する必要があります。
- 逸脱度R二乗(調整済み)
-
異なる数の項を持つモデルを比較する場合は、調整済み逸脱度R2を使用します。逸脱度R2はモデルに項を追加すると必ず大きくなります。調整済み逸脱度R2値にはモデルに含まれる項の数が組み入れられるため、正しいモデルの選択に役立ちます。
- AIC、AICc、BIC
-
異なるモデルを比較する際はAIC、AICc、BICを使用します。いずれの統計量でも、小さい値が好ましいと考えられます。ただし、予測変数セットに対して最小値を持つモデルは必ずしもデータに良好に適合しません。適合度検定と残差プロットも使用して、データに対するモデルの適合度を評価してください。
モデル要約
| 逸脱 (deviance) R二乗 | 逸脱 (deviance) R二乗 (調整済み) | AIC | AICc(修正済み 赤池情報量基準) | BIC(ベイズ 情報量基準) |
|---|---|---|---|---|
| 97.95% | 76.75% | 105.98 | 171.98 | 114.48 |
主要な結果:逸脱度R二乗、逸脱度R二乗(調整済み)、AIC
これらの結果を基に、モデルは、応答変数における合計逸脱度のおよそ97.95%を説明づけます。これらのデータでは、逸脱度R2の値は、モデルがデータに十分に適合することを示しています。追加モデルが異なる予測変数と適合する場合、調整済み逸脱度R2の値、AICの値、AICcの値、BICの値を使用して、追加モデルがどの程度データに適合するかを比較します。
ステップ5:データに適合しないモデルかどうかを判断する
- 不適切なリンク関数
- モデル内にある変数の高次項が省略されています
- モデル内にはない予測変数が省略されています
- 過分散
逸脱度が統計的に有意な場合、別のリンク関数を実行、あるいはモデル内の項を変更できます。
- 逸脱度:逸脱度検定のp値では、1行当たりの試行回数が1回に配置されているデータの方が、試行回数が複数回のデータよりも低い傾向があり、一般的には、試行回数が少なくなるほどp値も減少します。データフォーマットが1試行/行の場合は、ホスマー-レメショウ検定の結果の信頼度がより高くなります。
- ピアソン:ピアソン検定で使用する近似カイ二乗分布は、データに含まれる行ごとの事象の期待数が小さい場合は不正確になります。それゆえ、データのフォーマットが1試行/行の場合、ピアソンの適合度検定は不正確となります。
- ホスマー-レメショウ(Hosmer-Lemeshow):ホスマー-レメショウ検定は他の適合度検定のように、データ内の行ごとの試行回数にも左右されません。データの各行の試行回数がほとんどない場合、ホスマー-レメショウ検定は、データに対するモデルの適合度を示す指標として、信頼度が高まります。
応答情報
| 変数 | 値 | 計数 | 事象名 |
|---|---|---|---|
| 損傷 | 事象 | 506 | Event |
| 非事象 | 7482 | ||
| コンテナ | 合計 | 7988 |
適合度検定
| 検定 | 自由度 | カイ二乗 | p値 |
|---|---|---|---|
| 逸脱 (deviance) | 5 | 0.97 | 0.965 |
| ピアソン | 5 | 0.97 | 0.965 |
| Hosmer-Lemeshow | 6 | 0.10 | 1.000 |
事象 試行フォーマットの主要な結果:応答情報、逸脱度検定、ピアソン検定、ホスマー-レメショウ検定
これらの結果では、すべての適合度検定のp値は、通常の有意水準である0.05よりも大きいです。この検定は、二項分布が予測できないように、予測される確率が観測される確率から離れた値になることを示す根拠にはなりません。
