目的の方法または計算式を選択してください。
単体重心計画
成分がq個の混合に対する単体重心計画の計画点の数は、2**q - 1になります。計画点は次のような内訳になっています。
- 1つの成分xiが1で、他の成分は0のすべての点(x1, x2, ..., xq)で、頂点と呼ばれる。
- 1つの成分xiが1/2、別の成分xjが1/2、その他の成分は0のすべての点。
- 1つの成分xiが1/3、別の成分xjが1/3、xkが1/3、その他の成分は0のすべての点。
- このパターンが、全ての成分が1/qになるまで続きます。最終点(すべての成分が等しい)は計画の中心または重心と呼ばれます。
単体格子計画
単体格子計画では、格子次数mにq個の成分(変数)があります。次数mは1~10の値です。Minitabでは、次の計画を作成できます。
| 格子次数(m) | 成分数(q) |
|---|---|
| 1 | 2 - 20日 |
| 2 | 2 - 20日 |
| 3 | 2 - 17日 |
| 4 | 2 - 11日 |
| 5 | 2 - 8日 |
| 6 | 2 - 7日 |
| 7 | 2 - 6日 |
| 8 | 2 - 5日 |
| 9 | 2 - 5日 |
| 10 | 2 - 5日 |
極頂点計画
Minitabでは制約がある計画空間の極頂点をXVERTアルゴリズムで生成し、指定の次数までの重心点をピーペル(Piepel)のCONAEVアルゴリズムで算出します。詳細は、コーネル(Cornell)1およびセント・ジョン(St. John)2を参照してください。
- J.A. Cornell (1990). Experiments With Mixtures: Designs, Models, and the Analysis of Mixture Data, John Wiley & Sons.
- R.C. St. John (1984). "Experiments With Mixtures in Conditioning and Ridge Regression," Journal of Quality Technology 16巻, 81頁-96頁.
実験のタイプ
Minitabでは、3つのタイプの実験からデータを分析することができます。
| 種類 | 応答の依存性 |
| 混合 | 成分の相対比率のみに依存。 |
| 混合~プロセス変数 | 成分とプロセス変数に依存。プロセス変数は、混合の一部ではないものの、応答に影響する可能性がある実験中の因子です。 |
| 混合~量 | 成分の相対比率および混合成分の総量。 |
追補した計画での軸点の配置
計画の追補(点の追加)は、次のように行われます。点は、計画の中心と頂点との中間に配置されます。
計画を追補することで、辺上の点にのみ頼るのではなく計画内部の応答の情報を得ることができます。
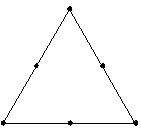
追補していない例
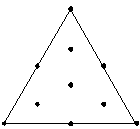
追補した例
成分の単位の変換
Minitabでは、計画は量、比率、および疑似成分単位で作成および分析することができます。
データの単位を量から比率に変換する計算式は以下です。
- 比率 = 量 / 合計
合計 = 1の場合、比率単位 = 量単位です。
単位を比率から疑似成分単位に変換する計算式は以下です。
- 疑似 = (比率 - 下限) / (1 - 下限の和)
- 比率 = 疑似 * (1 - 下限の和) + 下限
すべての下限 = 0の場合、疑似の単位 = 比率の単位です。
モデル項
混合計画には様々なタイプのモデル項が含まれます。それらの項と表記は以下です。
| モデル | 項 |
| 線形 | A B C |
| 2次 | 線形 + AB AC BC |
| 特殊3次 | 2次+ ABC |
| 完全3次 | 特殊3次 + AB(A-B) AC(A-C) BC(B-C) |
| 特殊4次 | 2次 + AABC ABBC ABCC |
| 完全4次 | 特殊4次 + AB(A-B) AC(A-C) BC(B-C) AB(A-B)2 AC(A-C)2 BC(B-C)2 |
混合計画には定数項は無いことに留意してください。逆項には1/A、1/B、1/Cなどが含まれます。
