目的の方法または計算式を選択してください。
係数(Coef)
Minitabでは、最小二乗推定値から係数が計算されます。
行列項において、係数の最小二乗推定値は以下のようになります。
b = (X'X)-1X'y
高次モデルの係数に関する詳細は、コーネル(Cornell)1を参照してください。
表記
| 用語 | 説明 |
|---|---|
| X | 計画行列 |
| y | 応答列 |
- J.A. Cornell (1990). Experiments With Mixtures: Designs, Models, and the Analysis of Mixture Data, John Wiley & Sons.
係数の標準誤差(SE Coef)
単回帰では係数の標準誤差は以下になります。
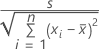
重回帰の係数の標準誤差はこの行列の対角要素の平方根です。
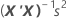
表記
| 用語 | 説明 |
|---|---|
| xi | i番目の予測変数の値 |
 | 予測変数の平均 |
| X | 計画行列 |
| X' | 計画行列の転置 |
| s2 | 誤差の平均平方 |
t値
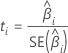
表記
| 用語 | 説明 |
|---|---|
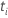 | 係数の検定統計量( 係数) 係数) |
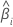 |  推定係数 推定係数 |
 | 推定係数の標準誤差( 推定係数) 推定係数) |
p値~係数表
回帰係数が0に等しいという帰無仮説の両面p値は以下になります。
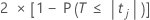
自由度は、以下に示す誤差に対する自由度です。
n – p
表記
| 用語 | 説明 |
|---|---|
 | 自由度を持つt分布の累積分布関数は、誤差に対する自由度に等しくなります。 |
| tj | j番目の係数のt統計量。 |
| n | データセットに含まれる観測値の数。 |
| p | 項の自由度の和。 |
分散拡大係数(VIF: Variance Inflation Factor)
VIFはそれぞれの予測変数を残りの予測変数について回帰分析し、R2値を割り出すことにより算出することができます。
計算式
予測変数xjの場合、VIFは以下のようになります。

表記
| 用語 | 説明 |
|---|---|
| R2( xj) | xjを応答変数、モデル内の他の項を予測変数とする決定係数 |
