平方和
距離の平方和です。ここで示す計算式は、因子AおよびBを持つ完全実施モデル、2水準モデルを求めるものです。これらの計算式は3つ以上の因子を持つモデルに展開することができます。詳細は、Montgomery1を参照してください。
全体平方和は、モデル内の変動の合計です。平方和(A)と平方和(B)は全体平均を中心とした推定因子水準平均を二乗した偏差の和です。誤差の平方和は、残差の平方和です。処理内の誤差とも呼ばれます。計算は次のようになります。

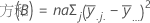
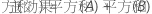

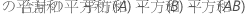
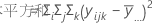
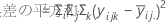
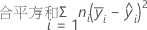



- D.C. Montgomery (1991). Design and Analysis of Experiments, Third Edition, John Wiley & Sons.
表記
| 用語 | 説明 |
|---|---|
| a | 因子Aの水準数 |
| b | 因子Bの水準数 |
| n | 合計反復数 |
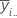 | 因子Aのi番目水準の平均 |
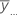 | すべての観測値の全体平均 |
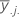 | 因子Bのj番目水準の平均 |
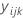 | 因子Aのi番目の水準、因子Bのj番目の水準、およびk番目の反復での観測値 |
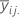 | 因子Aのi番目の水準および、因子Bのj番目の水準での平均 |
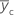 | 中心点の平均応答 |
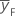 | 要因計画点の平均応答 |
| nF | 要因計画点の数 |
遂次平方和
Minitabでは、分散のSS回帰成分または処理成分を各因子の遂次平方和に分解します。遂次平方和は、因子や予測変数をモデルに入力するときの順序によって異なります。逐次平方和は、以前に入力された因子が何かある場合、1つの因子によって説明される回帰平方和の独特の部分です。
たとえば、X1、X2、X3という3つの因子または予測変数を含むモデルがある場合、X2の遂次平方和は、X1がモデル内にすでに含まれている場合、X2によって説明される残りの変動の割合を示します。別の平方和を得るには、分析を繰り返して異なる順序で因子を入力します。
調整平方和
調整平方和は、項をモデルに入力するときの順序に依存しません。調整平方和は、その他のすべての項が入力された順序にかかわらずモデル内に含まれる場合に、項によって説明される変動量を表します。
たとえば、3つの因子X1、X2、X3を扱うモデルがあった場合、X2の項が、調整平方和はX2の残りの変動にどれほど寄与しているのかを表します。モデル内のX1およびX3も同様です。
3つの因子の調整平方和の計算式は以下になります。
- SSR(X3 | X1, X2) = SSE (X1, X2) - SSE (X1, X2, X3)または
- SSR(X3 | X1, X2) = SSR (X1, X2, X3) - SSR (X1, X2)
上の式で、SSR(X3 | X1, X2)は、X1とX2がモデルに含まれる場合のX3の調整平方和です。
- SSR(X2, X3 | X1) = SSE (X1) - SSE (X1, X2, X3)または
- SSR(X2, X3 | X1) = SSR (X1, X2, X3) - SSR (X1)
上の式で、SSR(X2, X3 | X1)は、X1がモデルに含まれる場合のX2とX3の調整平方和です。
モデル1に4つ以上の因子がある場合はこの式を拡張して計算します。
- J. Neter、W. WassermanおよびM.H. Kutner(1985年)、Applied Linear Statistical Models第2版、Irwin, Inc.
自由度(DF)
因子AとB、およびブロック変数を持つ完全実施要因計画において、各平方和と関連付けられた自由度の数は次のように計算されます。


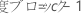

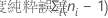


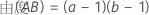

中心点を持つ2水準計画の場合、曲面性の自由度は1です。
表記
| 用語 | 説明 |
|---|---|
| a | 因子Aの水準数 |
| b | 因子Bの水準数 |
| c | ブロック数 |
| n | 合計観測数 |
| ni | i番目の因子水準の組合せの観測数 |
| m | 因子水準の組合せの数 |
| p | 係数の数 |
調整平均平方~項

F
交互作用と主効果が有意かどうかを判定するための検定です。モデル項の計算式は以下になります。
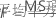
検定の自由度は以下になります。
- 分子 = 項の自由度
- 分母 = 誤差の自由度
Fの値が大きいほど、有意な効果は存在しないとする帰無仮説を棄却する根拠となります。
バランス型の分割実験計画では、変更が難しい因子のF統計量において、分母にプロット全体誤差の平均平方が使用されます。その他の分割実験計画では、平均平方の期待値に基づく分母にWP誤差とSP誤差の線形の組み合わせが使用されます。
p値~分散分析表
p値は自由度(DF)が以下であるF分布から計算される確率です。
- 分子DF
- 項の自由度の和、または検定内の項
- 分母DF
- 誤差に対する自由度
計算式
1 − P(F ≤ fj)
表記
| 用語 | 説明 |
|---|---|
| P(F ≤ f) | F分布についての累積分布関数 |
| f | 検定におけるF統計量 |
純粋誤差不適合検定
- 各反復セットにおける平均からの応答の偏差の平方和を合計し純粋誤差の平方和を生成
- 純誤差の平均平方
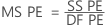

上の式で、nは観測値の数、mはx水準の組み合わせの数です。
- 不適合平方和
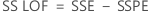
- 不適合平均平方

- 検定統計量

F値が大きい場合やp値が小さい場合は、そのモデルが不適切であると示唆しています。
p値~不適合検定
- 分子DF
- 不適合に対する自由度
- 分母DF
- 純粋誤差に対する自由度
計算式
1 − P(F ≤ fj)
表記
| 用語 | 説明 |
|---|---|
| P(F ≤ fj) | F分布についての累積分布関数 |
| fj | 検定におけるF統計量 |
