このトピックの内容
適合値
適合する値は、適合値または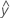 とも呼ばれます。適合値は、予測変数の標準偏差応答の点推定です。予測変数の値は、X値とも呼ばれます。
とも呼ばれます。適合値は、予測変数の標準偏差応答の点推定です。予測変数の値は、X値とも呼ばれます。
解釈
適合値は、データセットに含まれる観測値ごとの特定のx値をモデル式に入力することによって計算されます。
たとえば、式がln (y) = ln (5 + 10x)の場合に、X値が2ならば、適合値は3.21888 (ln(5 + 10(2)))となります。
観測された値と非常に異なる適合値を含む観測値は、異常な観測値である可能性があります。異常な予測値を持つ観測値は、影響力がある可能性があります。Minitabが、データに異常または影響力がある値が含まれていると判断した場合は、これらの観測値が特定された、異常な観測値の適合値と診断の表が出力されます。大きな標準化残差を持つ観測値は、提示された回帰式にしっかりと従っていません。ただし、いくつかの異常な観測値があることは予測されています。たとえば、大きな標準化残差の基準に基づくと、観測値の約5%は大きな標準化残差を持つとしてフラグがつけられることが予測されます。異常な値に関する詳細は、異常な観測値を参照してください。
元の応答の信頼区間(95%信頼区間)
これらの信頼区間は、モデルに含まれる因子や予測変数の観測値を持つ、母集団の標準偏差応答を含む可能性が高い値の幅です。
データのサンプルはランダムであるため、2つの母集団サンプルの信頼区間が同一である可能性は低くなります。しかし、サンプルを何度も繰り返して測定すると、得られた信頼区間の特定の割合に未知の母集団パラメータが含まれることになります。このようなパラメータを含む信頼区間の割合(%)を区間の信頼水準と言います。
- 点推定
- 点推定は、サンプルデータから算出されます。
- 誤差幅
- 誤差幅は、信頼区間の幅を定義し、サンプル、サンプルサイズ、信頼水準において観測された変動性によって決定します。
解釈
信頼区間を使用して、変数の観測値に関する適合値の推定値を評価します。
たとえば、信頼水準が95%の場合、モデルに含まれる因子や予測変数における特定の値の、母集団の標準偏差が信頼区間に含まれていることが95%信頼できます。信頼区間により、結果の実質的な有意性を評価しやすくなります。状況に応じた専門知識を利用して、信頼区間に実質的に有意な値が含まれているかどうかを判断します。信頼区間が広い場合、将来の値の標準偏差に対する信頼性が低くなります。信頼区間が広すぎて役に立たない場合、サンプルのサイズを増加させることを検討します。
比の残差
比の残差は、観測された標準偏差を適合値で割った値です。
Ln(標準)
観測された応答標準偏差の自然対数です。
Ln(適合値)
適合標準偏差の自然対数です。
標準誤差Ln(適合値)
適合標準偏差の自然対数の標準誤差は、指定した変数設定に対する標準偏差の推定値の変動を推定します。平均応答の信頼区間の計算には、適合値の標準誤差が使用されます。標準誤差は常に正数です。
解釈
適合値の標準誤差は、標準偏差の自然対数の推定値の精度を測定するために使用します。標準誤差が小さいほど、推定値の精度が高くなります。
変換済み応答の信頼区間(95%信頼区間)
これらの信頼区間は、モデルに含まれる因子や予測変数の観測値を持つ、母集団の標準偏差の自然対数を含む可能性が高い値の幅です。
データのサンプルはランダムであるため、2つの母集団サンプルの信頼区間が同一である可能性は低くなります。しかし、サンプルを何度も繰り返して測定すると、得られた信頼区間の特定の割合に未知の母集団パラメータが含まれることになります。このようなパラメータを含む信頼区間の割合(%)を区間の信頼水準と言います。
- 点推定
- 点推定は、サンプルデータから算出されます。
- 誤差幅
- 誤差幅は、信頼区間の幅を定義し、サンプル、サンプルサイズ、信頼水準において観測された変動性によって決定します。
解釈
信頼区間を使用して、変数の観測値に関する適合値の推定値を評価します。
たとえば、信頼水準が95%の場合、モデルに含まれる因子や予測変数における特定の値の、母集団の対数標準偏差が信頼区間に含まれていることが95%信頼できます。信頼区間により、結果の実質的な有意性を評価しやすくなります。状況に応じた専門知識を利用して、信頼区間に実質的に有意な値が含まれているかどうかを判断します。信頼区間が広い場合、将来の値の標準偏差に対する信頼性が低くなります。信頼区間が広すぎて役に立たない場合、サンプルのサイズを増加させることを検討します。
Ln(残差)
観測された応答標準偏差の自然対数と適合標準偏差の自然対数との差です。比の残差の対数です。
解釈
対数残差は、モデルで説明されない応答(出力)データの部分を表します。Minitabが変動性の分析で算出する残差タイプの中で、対数残差は通常の残差と最もよく似ています。
標準Ln(残差)
自然対数の標準化残差は、対数残差をその(漸近の)標準誤差で割ったものに等しくなります。
解釈
自然対数の標準化残差を使用すると、外れ値を検出しやすくなります。標準Ln(残差)の値が-2~2の場合は、データには異常な観測値はありません。
2より大きく、-2より小さい標準化残差は、通常は大きなものであると見なされます。ラベルがつけられた観測値は、提示された回帰式にしっかりと従っていません。ただし、いくつかの異常な観測値があることは予測されています。たとえば、大きな標準化残差の基準に基づくと、観測値の約5%は大きな標準化残差を持つとしてフラグがつけられることが予測されます。詳細は、異常な観測値を参照してください。
標準化残差が役に立つのは、生の残差が外れ値を識別するものとして許容されない場合があるためです。生の残差の分散は、それに関連づけられたx値によって異なることがあります。この残差の不一致では、生の残差の大きさを評価するのが難しくなります。残差を標準化することで、異なる分散が共通の尺度に変換され、この問題は解消されます。
Hi (てこ比)(I)
てこ比は、観察値のx値からデータセット内のすべての観察値のx値の平均までの距離を測定します。
解釈
てこ比値は0から1の間の値で、Minitabの異常な観測値の適合値と診断の表では、観測値のてこ比値が3p/nまたは0.99のいずれか小さい方を超えていることがXという文字によって示されます。3p/nでは、pはモデル内の係数の数で、nは観測値の数を表します。Minitabで「X」とラベル付けされる観測値は、影響力がある可能性があります。
影響力のある観測値は、モデルに対し不均衡な影響を与えるので、誤解を招く結果が生じる可能性があります。たとえば、影響力のある点を含める、または除外することにより、係数が統計的に有意かどうかが変わることがあります。影響力のある観測値は、てこ比点、外れ値またはその両方である可能性があります。
影響力のある観測値を確認する場合、観測値がデータ入力エラーまたは測定エラーでないかどうかを調べます。観測値がデータ入力エラーでも測定エラーでもない場合、観測値の影響度を調べます。まず、観測値のあるモデルとないモデルを適合します。その後、係数、p値、R2やその他のモデルの情報を比較します。影響力のある観測値を除外したときにモデルが大きく変化する場合は、モデルをさらに調べて、モデルの指定が誤っていないかどうかを確認します。問題を解決するには、さらに多くのデータを集めることが必要な場合もあります。
クックの距離(D)
クックの距離(D)は、一般線形モデルにおける係数のセットに対して観測値が持つ影響力を測る測度です。クックの距離は、観測値の影響力を判定するために、各観測値のてこ比値と標準化残差が考慮されます。
解釈
D値が大きい観測値は、影響力がある可能性があります。D値が大きい場合の一般的な基準は、D値がF分布の中央値であるF(0.5, p, n-p)よりも大きいときです。ここで、pはモデル項の数(定数も含む)で、nは観測値の数です。D値を調べるもう1つの方法は、個別値プロットなどのグラフを使用して値を比較することです。D値が他に比べて大きい観測値は、影響力がある可能性があります。
影響力のある観測値は、モデルに対し不均衡な影響を与えるので、誤解を招く結果が生じる可能性があります。たとえば、影響力のある点を含める、または除外することにより、係数が統計的に有意かどうかが変わることがあります。影響力のある観測値は、てこ比点、外れ値またはその両方である可能性があります。
影響力のある観測値を確認する場合、観測値がデータ入力エラーまたは測定エラーでないかどうかを調べます。観測値がデータ入力エラーでも測定エラーでもない場合、観測値の影響度を調べます。まず、観測値のあるモデルとないモデルを適合します。その後、係数、p値、R2やその他のモデルの情報を比較します。影響力のある観測値を除外したときにモデルが大きく変化する場合は、モデルをさらに調べて、モデルの指定が誤っていないかどうかを確認します。問題を解決するには、さらに多くのデータを集めることが必要な場合もあります。
DFITS
DFITSは、一般線形モデルにおける適合値に対して各観測値が持つ影響力を測る測度です。DFITSは、各観測値をデータセットから取り除きモデルを再度適合させたときに適合値が変化するおおよその標準偏差を表します。
解釈
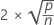
| 用語 | 説明 |
|---|---|
| p | モデルの項の数 |
| n | 観測値数 |
影響力のある観測値を確認する場合、観測値がデータ入力エラーまたは測定エラーでないかどうかを調べます。観測値がデータ入力エラーでも測定エラーでもない場合は、観測値の影響力を判断します。まず、観測値があるモデルとないモデルを適合します。その後、係数、p値、R2やその他のモデルの情報を比較します。影響力のある観測値を除外したときにモデルが大きく変化する場合は、モデルの指定に間違いがないかどうかをさらに調べます。問題を解決するには、さらに多くのデータを集めることが必要な場合もあります。
