別名構造とは
別名構造は、計画において発生する交絡パターンを記述するものです。互いに交絡する項は「別名関係にある」とも言います。
別名、または交絡は、計画には因子水準のすべての組み合わせは含まれないため、一部実施要因計画において発生します。たとえば、因子Aが三元交互作用BCDと交絡する場合、Aの効果の推定値は、Aの効果とBCDの効果の合計になります。有意な効果がAによるものかBCDによるものか、あるいはその両方の組み合わせによるものかを特定できません。Minitabにおける計画の分析では、モデルに交絡項を追加することができます。項リストの後の方の項が削除されます。ただし、特定の項は常に最初に適合されます。たとえば、モデルにブロックを追加した場合、Minitabはブロック項が維持され、ブロックと別名関係にある項が削除されます。
- 計画に含まれる因子の数が7以下の場合、別名構造は、別名関係にある項をすべて表示します。
- 計画に含まれる因子の数が8~10の場合は、別名構造は、3因子交互作用までの別名の項を表示します。
- 計画に含まれる因子の数が11~15の場合は、別名構造は、2因子交互作用までの別名の項を表示します。
一部実施計画の別名構造
一部実施要因計画では、因子の項はそれぞれを個別に推定することはできません。別名関係にある項を調べるために、別名構造を使用します。
解釈
- 外科医: 入院中を通して、外科医が患者に付き添うかどうか
- VAS: 病院のスタッフが、患者の痛みのレベルを調べるのに視覚的アナログ尺度を使用するかどうか
- イブプロフェン: 鎮痛剤としてイブプロフェンが使用されるかどうか
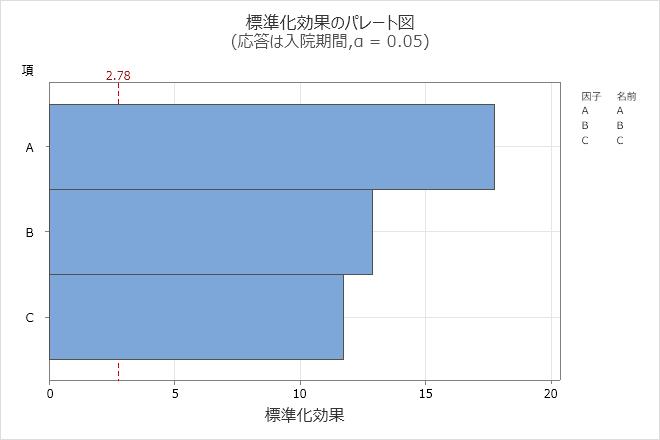
効果のパレート図は全ての因子が水準0.05において統計的に有意であることを示していますが、別名構造は主効果が2因子交互作用と別名構造にあることを示しています。
交絡構造
| 因子 | 名前 |
|---|---|
| A | 外科医 |
| B | VAS |
| C | イブプロフェン |
| 別名 |
|---|
| I + ABC |
| A + BC |
| B + AC |
| C + AB |
これらのデータでは、パレート図でAと示された効果は外科医の主効果か、イブプロフェン*VASの交互作用効果なのか、あるいは両方の組み合わせを意味する可能性があります。別名であるために、Minitabでは因子Aと、BC間の交互作用の両方は同じモデルに含まれません。これらの効果を区別するため、研究者は計画を折り重ねて実験の実行数をさらに増やすこともできます。折り重ねに関する詳細については、折り重ねとはを参照してください。
ブロック化した計画の別名構造
計画において、反復よりもブロックの方が多い場合、いくつかの項はブロックの項と別名関係にあります。
解釈
- 外科医: 入院中を通して、外科医が患者に付き添うかどうか
- VAS: 病院のスタッフが、患者の痛みのレベルを調べるのに視覚的アナログ尺度を使用するかどうか
- イブプロフェン: 鎮痛剤としてイブプロフェンが使用されるかどうか
研究者はこれらのデータを短期間では収集できないため、ブロックを使用して、たとえば患者毎のセメントの違いなど、異なる条件下で得られる情報の差異を説明します。別名構造は、ブロックの項が3因子の交互作用の項と別名関係にあることを表しています。Minitabにおける計画の分析では、ブロックの項が交互作用よりも先にモデルに追加されます。つまり、モデルにブロックの項が含まれている場合、ABC交互作用はモデルには追加されません。
交絡構造
| 因子 | 名前 |
|---|---|
| A | 外科医 |
| B | VAS |
| C | イブプロフェン |
| 別名 |
|---|
| I |
| ブロック1 - ABC |
| ブロック2 + ABC |
| ブロック3 - ABC |
| A |
| B |
| C |
部分的な別名関係を持つ計画の別名構造
別名は、計画に因子水準の組み合わせの一部しか含まれていないときに発生します。別名構造では、完全に別名の項に1に等しい係数があります。例えば、因子Aが三元交互作用BCDと交絡する場合、Aの効果の推定値は、Aの効果とBCDの効果の合計になります。有意な効果がAによるものかBCDによるものか、あるいはその両方の組み合わせによるものかを特定できません。同じモデルで完全に別名の項を含める場合、項のリストの後ろにリスト化される完全に別名の項は削除されます。
部分的な別名は、共変量を持つ要因計画、二値応答を持つ要因計画、およびPlackett-Burman計画で発生します。部分的な別名関係では、別名構造内の項に1以外の係数の存在が可能です。部分的な別名関係のある項を解釈する際は注意してください。別名表の係数は、その項が、モデル内の項の推定値をどの程度偏らせるかを示しています。
解釈
- 外科医: 入院中を通して、外科医が患者に付き添うかどうか
- VAS: 病院のスタッフが、患者の痛みのレベルを調べるのに視覚的アナログ尺度を使用するかどうか
- イブプロフェン: 鎮痛剤としてイブプロフェンが使用されるかどうか
共変量は患者の年齢です。患者の年齢は入院日数に重要な変数ですが、実験の実行の度に患者の年齢をコントロールすることはできません。別名構造は、いくつかの交互作用が部分的に他の項と別名関係にあることを示しています。例えば、2行目はAの主効果が交互作用AB、AC、BC、およびABCと部分的に別名関係にあることを示しています。最終行では、Cの主効果はABの交互作用と完全に交絡していることを示しています。
交絡構造
| 因子 | 名前 |
|---|---|
| A | 外科医 |
| B | VAS |
| C | イブプロフェン |
| 別名 |
|---|
| I + 0.91 AB - 0.23 AC - 1.37 BC + 0.27 ABC |
| A + 0.61 AB - 0.15 AC - 0.41 BC - 0.15 ABC |
| B + 0.04 AB + 0.49 AC - 0.07 BC - 0.01 ABC |
| C + AB |
