目的の方法または計算式を選択してください。
このトピックの内容
逸脱度
逸脱度は、現在のモデルと完全モデルの誤差を測定します。完全モデルは、n個のパラメータ(観測値ごとに1つのパラメータ)があるモデルです。完全モデルは対数尤度関数を最大化します。完全モデルは、nよりも少ないパラメータを持つモデルの類似点を導き出します。完全モデルの比較では、スケール逸脱度を使用します。


以下の式では、二項モデルのスケール逸脱度への寄与度を求めます。
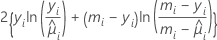
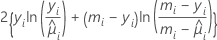
検定の自由度は、サンプルのサイズやモデル内の項数によって変わります。

表記
| 用語 | 説明 |
|---|---|
| Lf | 完全モデルの対数尤度 |
| Lc | 完全モデルのサブセットの項を持つモデルの対数尤度 |
| yi | データ内のi行目の事象数 |
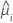 | データ内のi行目の推定平均応答 |
| mi | データ内のi行目の試行数 |
| n | データの行数 |
| p | 回帰自由度 |
ピアソン
一般化されたピアソンカイ二乗統計量は、観測値と適合値の相対的な差を評価します。
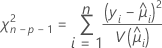
検定の自由度は、サンプルのサイズやモデル内の項の数によって変わります。ピアソン統計量には、正規データの正しいカイ二乗分布があります。非正規データの場合、二項分布とポアソン分布のように、統計量は漸近的に分布に近似します。
表記
| 用語 | 説明 |
|---|---|
| n | データの行数 |
| p | 回帰自由度 |
| yi | i番目の因子・共変量パターンの応答値 |
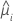 | i行目の推定平均応答 |
| V(·) | モデルの分散関数(以下で定義されます) |
次の式では二項モデルの分散関数が算出されます。
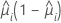
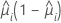
ホスマー-レメショウ
2値応答を持つモデルの適合度検定は、推定確率によるグループデータに基づきます。これは、観測期待度数と推定期待度数の2 × g表(gはグループ数)から得られるカイ二乗統計量です。検定の自由度はg − 2です。
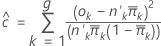
計算式は以下になります。
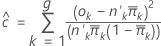
グループを形成するには、Minitabは推定確率を順位づけして、サイズが等しい10のグループの作成を試します。
グループ内にある事象の期待数は以下になります。
期待事象 = 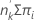
非事象数の期待値は以下になります。
期待非事象 = 
表記
| 用語 | 説明 |
|---|---|
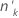 | k番目のグループ内の試行回数 |
| ok | 以下の中にある事象数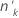 因子・共変量パターン 因子・共変量パターン |
 | 各グループの平均推定確率 |
| πi | グループ内の因子・共変量パターンの適合確率 |
