テューキーの方法は、指定した水準になるように全体過誤率を制御しながら、因子水準平均間のすべてのペアの差の信頼区間を作成するために、分散分析で使用されます。多重比較を行う際は、全体過誤率を考慮することが重要になります。これは、一連の比較で第1種の過誤を犯す確率が、一度だけ比較する場合の過誤率よりも高くなるからです。この高い過誤率に対処するため、テューキーの方法では、個々の信頼区間ごとに信頼水準を調整し、生成される同時信頼水準と指定した値とが等しくなるようにしています。
テューキー信頼区間の例
メモリチップの応答時間を測定するとします。5社のメーカーから25個のチップを抽出しました。
5つの工場間の10すべての比較を調べ、具体的にどの平均が異なっているのかを判断することにします。テューキーの方法を使用して、比較全体の全体過誤率が0.05(95%の同時信頼水準と同等)になるように指定します。Minitabでは、95%の同時信頼水準を得るのに、個別の信頼水準10個を99.35%にする必要があると計算します。このようにしてテューキーの信頼区間の幅を広くすると母数の推定値の精度が低下しますが、1つ以上の信頼区間に真の差が含まれない確率は最大5%に制限されます。この内容を理解したうえで、次に信頼区間を調べ、ゼロを含む(有意な差を示唆する)信頼区間がないかを確認できます。
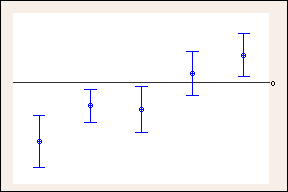
個別の信頼水準が95%の信頼区間
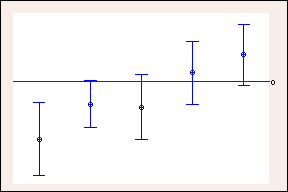
テューキーの方法を使用して95%の同時信頼水準を得るために個々の信頼水準を99.35%にした信頼区間
95%の信頼区間と上の例のテューキーの方法で使用した幅の広い99.35%の信頼区間の比較。0の参照線は、幅の広いテューキーの信頼区間によって結論がいかに変わるかを示しています。ゼロを含む信頼区間は、差がないことを示します。(スペースを考慮して、10の比較のうち5つのみを示しています)
