多変量分散分析（MANOVA）とは
多変量分散分析（MANOVA）は、複数の応答変数と、共通な一連の予測変数との間の関係を同時に分析する検定です。分散分析と同様、多変量分散分析でも連続応答変数とカテゴリ予測変数が必要です。多変量分散分析では、複数の分散分析を実行して応答変数を1つずつ調べていくのに比べ、重要な利点がいくつかあります。
- 検出力の増加
- 応答変数間でのデータの共分散構造を使用して、平均の同等性を同時に検定できます。応答変数が相関していれば、この情報が、個々の分散分析（ANOVA）では小さ過ぎて特定できない違いを見つけるのに役立ちます。
- 多変量応答パターンを検出
- 因子は、単一の応答に影響を与えるのではなく応答間の関係に影響を与える可能性があります。次の図で示しているように、分散分析（ANOVA）ではこうした多変量パターンは検出されません。
- 全体過誤率を管理
- 分散分析（ANOVA）では、繰り返すごとに帰無仮説を誤って棄却する確率が高くなります。多変量分散分析（MANOVA）ですべての応答変数を同時に検定すれば、全体過誤率はα水準と同等になります。
たとえば、自社の建築製品用に異なる合金（1、2、3）の強度と柔軟性の影響を調べていたとします。最初に2種類の分散分析（ANOVA）を実行しましたが、結果は有意ではありませんでした。驚いて、両方の応答変数を個別値プロットにプロットしました。これらのプロットでは、有意でない分散分析の結果を視覚的に確認できます。
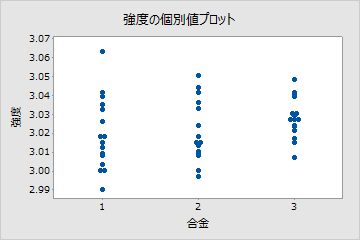
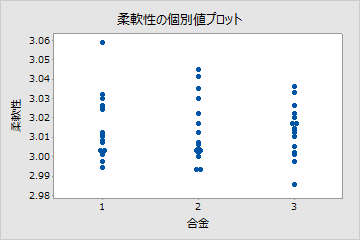
プロットでは、応答変数が相関していました。そこで多変量分散分析を実行することにしました。このときには0.05未満のp値が得られ、有意な結果となりました。散布図を作成すると、結果をよりよく理解できます。
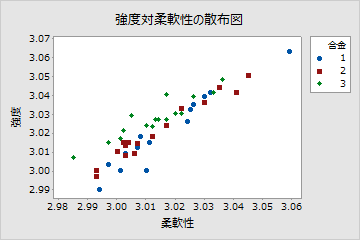
個別値プロットは、単変量の視点から合金が製品の強度と柔軟性のどちらにも影響しないことを表しています。しかし、同じデータを使った散布図では、異なる合金がこれらの2つの応答値の間の関係に変化を及ぼしていることがわかります。つまり、指定された柔軟性のスコアでは、合金1と2に比べ、合金3が全体的に高い強度を示しています。分散分析（ANOVA）ではこのような多変量応答を検出できませんが、多変量分散分析（MANOVA）では可能です。
注
通常、分析を実行する前にデータをグラフ化する必要があります。これによって、どの手法をとるのが適切かを判断するのに役立ちます。
多変量分散分析（MANOVA）に含まれる多変量検定
Minitabでは、モデル内の各項と特に求められる項に対して、自動的に4つの多変量検定が実行されます。
- ウィルクの検定
- ローリー-ホテリングの検定
- ピライの検定
- ロイの最大根検定
4つの検定はすべて、次の2つのSSCP（平方和と積和）行列に基づいています。
- 各項に関連付けられたH（仮説）行列。サンプル間平方和とも呼ばれます。
- 検定の誤差に関連付けられたE（誤差）行列。サンプル内平方和とも呼ばれます。
仮説行列を要求すると、SSCP（平方和と積和）行列が表示されます。
検定統計量は、HまたはE、あるいはその両方、またはE-1 Hの固有値のいずれかの形式で表記できます。これらの固有値の表示を要求することもできます。（固有値が繰り返される場合は対応する固有ベクトルが一意なものではなく、この場合、Minitabが表示する固有ベクトルと本やその他のソフトウェア内の固有ベクトルは一致しません。ただし、多変量分散分析検定は常に一意です。）
