このトピックの内容
平均の分析とは
平均の分析は、分散分析のグラフ版と言うべきもので、母集団平均が等しいことを検定します。グラフは、各因子水準平均、全体平均、および決定限界を表示します。点が決定限界の外側にある場合は、その点によって表される因子水準平均が全体平均と有意に異なることの証拠になります。
たとえば、温度と添加剤の設定が製品の評価にどれだけ影響を与えるかを調べるとします。実験後、平均の分析を使用して以下のグラフを生成します。
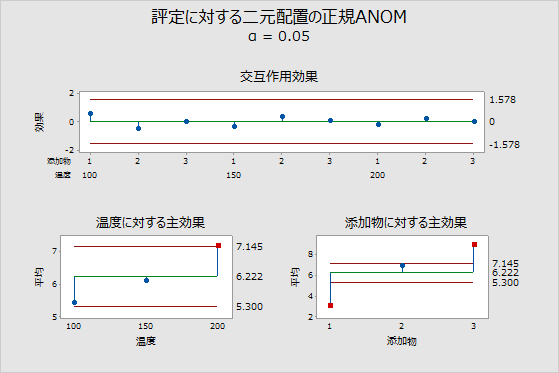

上のプロットでは、交互作用の効果が十分に決定限界内にあることが示されており、交互作用の証拠はありません。下方の2つのプロットは、2つの因子の水準平均を示し、平均と中心線の差が主効果です。左下のプロットでは、因子「温度」の3番目の平均が赤で表示されていますが、これはα = 0.05の場合に温度「200」の平均が全体の平均と有意に異なることを示しています。因子「添加剤」の水準1および3の主効果は、右下のプロットの決定限界の十分外側にあり、これらの平均が全体の平均と異なることを示す有意な証拠があることを示しています。
平均の分析(ANOM)と分散分析(ANOVA)の比較
分散分析は、処理平均が互いに異なるかどうかを検定します。平均の分析は、処理平均が全体平均と異なるかどうかを検定します。
多くの場合、両方の分析によって類似の結果が得られます。ただし、結果が異なるシナリオもいくつかあります。
- 平均の1つのグループが全体の平均を上回り、平均の別のグループが全体平均を下回る場合は、平均分析(ANOM)では示されなくても、分散分析(ANOVA)では差の証拠が示される可能性があります。
- あるグループの平均が他方の平均から離れている場合、分散分析のF-検定では差がないと結論され、平均分析(ANOM)ではそのグループと全体平均とに差があると結論される可能性があります。
さらに重要な違いとして、分散分析(ANOVA)ではデータが正規分布に従うと仮定するのに対して、平均分析(ANOM)では正規分布、二項分布、またはポアソン分布に従うデータに使用することができます。
