共変量とは
共変量は通常、分散分析(ANOVA)とDOEで使用されます。これらのモデルでは、共変量は任意の連続変数で、データ収集の際は基本的に制御されていません。共変量を含むことで、入力された変数をモデルに含めたり調整したりできるようになります。この変数は、実験において測定されてはいますが、ランダム化や制御はされていません。共変量を追加することでモデルの精度を大きく高めることができ、さらには最終的な分析結果にも大きな影響を与えます。また、モデル内の誤差が削減され、因子検定の検定力も上がります。一般的な共変量として、処理を適用する前の検査対象物の周辺温度、湿度、特性などがあります。
たとえば、技師が4種類の鉄の梁に見られる腐食の度合いを分析するとします。各梁を液体処理して腐食を早めることにしましたが、液体の温度を調整することはできません。つまり、このモデルで考慮すべき共変量は温度ということになります。
DOEで、2つの異なる種類のペンキが乾くまでの時間に対する共変量「周辺温度」の影響を調べるとします。
一般線形モデルへの共変量の追加例
ある繊維会社が3つの異なる機械を使用してモノフィラメント繊維を製造しているとします。どの機械を使用するかによって繊維の破壊強度が変化するかどうか判断したいと考えています。それぞれの機械で製造した繊維のうちランダムに5つずつ選び出し、強度と直径に関するデータを収集します。繊維の強度はその直径に関係しているため、可能な共変量として繊維の直径も記録します。
| C1 | C2 | C3 |
|---|---|---|
| 機械 | 直径 | 強度 |
| 1 | 20 | 36 |
| 1 | 25 | 41 |
| 1 | 24 | 39 |
| 1 | 25 | 42 |
| 1 | 32 | 49 |
| 2 | 22 | 40 |
| 2 | 28 | 48 |
| 2 | 22 | 39 |
| 2 | 30 | 45 |
| 2 | 28 | 44 |
| 3 | 21 | 35 |
| 3 | 23 | 37 |
| 3 | 26 | 42 |
| 3 | 21 | 34 |
| 3 | 15 | 32 |
- 共変量と応答が線形関係にあることを確認します。 Minitabでは、データを適合線プロットで分析することで実行できます。
- を選択します。
- 応答(Y)に、強度と入力します。
- 予測変数(X)に、直径と入力します。
- データが適合線とどれだけ近似しているか、R2が「完全な適合値」(100%)とどれだけ近似しているかを評価します。
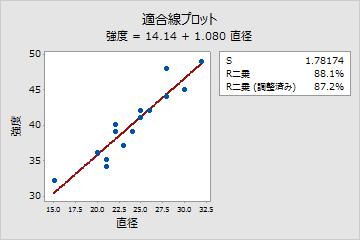
適合線プロットは、直径と強度の間に強い線形関係(87.2%)があることを示しています。
- 共変量を使用してGLM分析を実行します。
- を選択します。
- 応答に強度を入力します。
- 因子に機械を入力します。
- 共変量に直径を入力します。
- OKをクリックします。
繊維の製造データの場合、Minitabでは次の結果が表示されます。
一般線形モデル:強度 対 直径, 機械
分散分析 調整平 要因 自由度 調整平方和 均平方 F値 p値 直径 1 178.014 178.014 69.97 0.000 機械 2 13.284 6.642 2.61 0.118 誤差 11 27.986 2.544 不適合 7 18.486 2.641 1.11 0.487 純誤差 4 9.500 2.375 合計 14 346.400機械のF-統計量は2.61で、p値は0.118です。p値が0.05よりも大きいため、5%の有意水準で、使用する機械によって繊維の強度は変化しないという帰無仮説を棄却できません。繊維の強度はすべての機械で同じであると仮定できます。直径(共変量)のF-統計量は69.97のとき、p値は0.000である点に注意してください。これは、共変量の影響が有意であることを示しています。つまり、直径は繊維の強度に対して統計的に有意な影響を与えます。
ここで、分析を再実行して共変量を省略するとします。この場合、次の出力が得られます。
一般線形モデル:強度 対 機械
分散分析 調整平 調整平 要因 自由度 方和 均平方 F値 p値 機械 2 140.4 70.20 4.09 0.044 誤差 12 206.0 17.17 合計 14 346.4F-統計量が4.09のとき、p値が0.044である点に注意してください。モデルに共変量がなければ、5%の有意水準で帰無仮説を棄却し、繊維の強度は使用する機械によって変化すると結論付けてしまいます。
この結果は、共変量を使用して分析を実行した場合の結論と真逆です。この例は、共変量を含めないと誤った分析結果を導いてしまう可能性を示しています。
