一元配置分散分析（ANOVA）における多重比較の方法と計算式

Minitabには、一元配置分散分析において複数因子の平均値を比較するために、Tukey法、Fisher法、Dunnett法、HsuのMCB法、Games-Howell法の5つの方法があります。これらの検定に使われる計算式は以下です。

表記

用語	説明
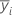	i番目の因子水準のサンプル平均
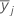	j番目の因子水準のサンプル平均
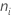	水準iの観測値の数
r	水準の数
s	併合標準偏差またはsqrt(MSE)
u	誤差に対する自由度
α	第一種過誤を発生する同時確率
α*	第１種過誤が発生する個別確率

[Tukey]:

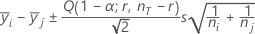
上の式で、Qは、自由度rとn_T - rでステューデント化された範囲分布の上位α番目の百分位です。

同時過誤率から個別過誤率を抽出するには以下の計算式を使用します。

[Fisher]:

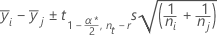
上の式で、tはステューデントのt分布における上位α/2番目の点で自由度はuです。

個別過誤率から同時信頼水準を抽出するには以下の計算式を使用します。

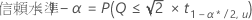
[Dunnett]:

dの計算方法については、63ページのHsu¹を参照してください。

[HsuのMCB]:

グループサイズがすべてnに等しい場合の計算式を提示しています。グループサイズが等しくない場合の計算式はHsu¹に示します。最良値を最大平均として選択し、かつi番目の平均値の信頼区間からその他の中の最大値を引いた値を求めたいと仮定します。

エンドポイントの下限が0より小さく、また

エンドポイントの上限が0より大きく、また

dの計算方法については、83ページのHsu¹を参照してください。

最適値が水準平均の中で最小値の場合、最大値が最小値に置き換わる以外は、計算式は同じです。

[Games-HowellとWelch検定]:

Welch検定の統計量は以下のように計算されます。

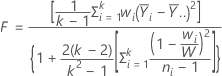
Welch検定におけるp値は、分子自由度k - 1の、F分布に対する上側確率です。kは水準Xの数、かつ分母自由度は以下から得られます。

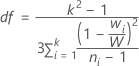
μ_i - μ_jの比較区間は以下です。

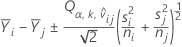
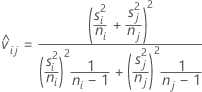
調整済p値の計算に使用するt率は以下の計算式と同等です。

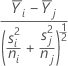
上の式で、

i番目のカテゴリ因子水準に対するj番目の応答は以下の計算式と同等です。

Y_ij, j = 1, ... , n_i; i = 1, ... k

i番目の水準での平均応答は以下の計算式と同等です。

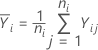
サンプル分散は以下の計算式と同等です。

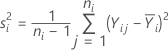
i水準の重み値は以下の計算式に同等です。

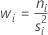
全重みの合計は以下の計算式に同等です。

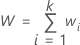
応答の総合的な重み付平均は、以下の計算式と同等です。

謝辞

多重比較の作成および実施にあたり、Jason C. Hsu氏にご協力いただきましたことに、感謝の意を表します。

[1] J.C. Hsu (1996).　多重比較　理論と方法　 Chapman & Hall