目的の方法または計算式を選択してください。
表記
この表記は一元配置分散分析の理解に大変重要です。以下に一元配置分散分析に使用する表記を記載します。
| 用語 | 説明 |
|---|---|
| r | 因子水準数 i = 1 ...r |
| i | 所定の因子水準 |
| j | 特定の因子水準に与えられたケース j = 1 ...ni |
| yij | 因子水準i番目の応答となるj番目の観測値 |
| ni | i番目の因子水準の観測値数 |
| nT | ケース合計数 |
| μi | 因子水準i番目での観測値の真の平均 |
| yi. | 因子水準i番目での観測値の合計数 |
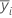 | i番目因子の応答平均 |
モデルの当てはめ
計算式
一元配置分散分析のモデルはいくつかの方法で指定できます。セル平均のモデルは以下の通りです。
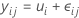
因子水準の観測値は全て同じ期待値μiです。μiは定数であるため、因子水準に関わらず観測値は全て分散が同じです。
分散分析において、モデルのあてはめとパラメータ推定値μiの導出には最小二乗推定法が使用されます。
一元配置分散分析の仮説検定手法は以下の通りです。
H0:μ1 = μ2= … = μr
H1:少なくとも一つ以上の平均値が他と等しくない
表記
| 用語 | 説明 |
|---|---|
| μi | 因子水準i番目での真の観測値平均またはパラメータ |
| εij | 平均値0および定数分散σ2で個別および正規分布に従った誤差 |
