このトピックの内容
ステップ1:グループの平均値間の差が統計的に有意かどうかを判断する
- p値 ≤ α:いくつかの平均値の間の差は統計的に有意です
- p値が有意水準以下の場合は、帰無仮説を棄却し、一部の母集団平均が等しくないと結論付けます。専門知識に基づいて、差が実際に有意かどうかを判断します。詳細は、統計的有意性と実際的有意性を参照してください。
- p値 > α:平均値の間の差は統計的に有意ではありません
- p値が有意水準より大きい場合、母集団の平均がすべて等しいという帰無仮説を棄却する十分な証拠を得られません。検定の検出力が、実質的に有意な差を検出するのに十分であることを確認します。詳細は、仮説検定の検出力を増やすを参照してください。
分散分析
| 要因 | 自由度 | 調整平方和 | 調整平均平方 | F値 | p値 |
|---|---|---|---|---|---|
| 塗料 | 3 | 281.7 | 93.90 | 6.02 | 0.004 |
| 誤差 | 20 | 312.1 | 15.60 | ||
| 合計 | 23 | 593.8 |
主要な結果:p値
この結果では、帰無仮説は4つの塗料の平均硬度値が等しいことを示しています。p値が有意水準0.05よりも低いことから、帰無仮説を棄却し、いくつかの塗料の平均値が異なっていると結論付けることができます。
ステップ2: グループの平均値について調べる
区間プロットを使用して、各グループの平均値と信頼区間を表示します。
- ドットはサンプル平均を示します。
- 各区間はグループ平均について95%の信頼区間です。グループ平均がそのグループの信頼区間に含まれることを95%信頼できます。
重要
多重比較を実施すると第1種過誤率が増加するため、区間の解釈は慎重に行ってください。つまり比較の回数を増やすと、少なくとも1つの比較結果において、観測された差が有意に異なっていると、誤って結論付ける確率も高まります。
プロットに表示される差を評価するために、グループ化情報表とステップ3で示すその他の比較出力を使用します。
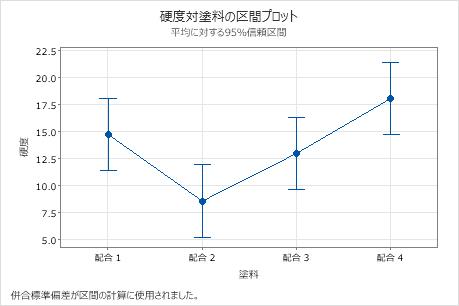
この区間プロットでは、配合2は最小の平均値、配合4は最大の平均値がでした。このグラフからは、いずれの差についても、統計的に有意であるかどうかは判断できません。統計的優位性を判断するために、平均の差に対する信頼区間を検討します。
ステップ3:グループ平均を比較する
一元配置分散分析のp値が有意水準より小さいとき、グループ平均の差が異なることはありますが、どのペアかは分かりません。グループ化情報表と平均の差の検定を用い、特定のグループペア間の平均差が統計的に有意かどうかを判断し、その差がどの程度なのかを推定します。
比較手法に関する詳細は、多重比較を用いた実際的かつ統計的な有意性の評価を参照してください。
- グループ化情報表
-
グループ化情報表を用い、いずれかのグループペア間の平均差が統計的に有意であるかどうかを素早く判断します。
文字を共有しないグループは、有意差があります。
- 平均の差検定
-
信頼区間を用い、差が含まれる可能性が高い範囲を特定し、これらの差が実質的に有意かどうかを判断します。表は、平均ペア間の差の信頼区間の一組を示しています。平均の差の区間プロットには同じ情報が表示されます。
0を含まない信頼区間は、統計的に有意な平均差を示しています。
選択した比較手法によって、表は異なるグループペアを比較し、以下のいずれかの信頼区間を表示します。-
個別信頼水準
分析が2回以上繰り返された場合に、1つの信頼区間に1つのグループペアの平均の真の差が含まれる回数の割合。
-
同時信頼水準
分析が2回以上繰り返された場合に、信頼区間のセットにすべてのグループの比較の真の差が含まれる回数の割合。
同時信頼水準を制御することは、多重比較を実行する場合に特に重要です。同時信頼水準を制御しない場合、少なくとも1つの信頼区間に真の差が含まれない確率は、比較の回数に応じて増加します。
-
詳細は、多重比較における個別および同時信頼水準を理解するを参照してください。
HsuのMCB法の結果の解釈方法についての詳細は、HsuのMCB(最良値との多重比較)とはを参照してください。
Tukey法と95%信頼水準を使用したグループ化情報
| 塗料 | N | 平均 | グループ化 | |
|---|---|---|---|---|
| 配合 4 | 6 | 18.07 | A | |
| 配合 1 | 6 | 14.73 | A | B |
| 配合 3 | 6 | 12.98 | A | B |
| 配合 2 | 6 | 8.57 | B | |
主要な結果:平均値とグループ化
この結果では、グループAは配合1、3、4を含み、グループBは配合1、2、3を含み、配合1と3はどちらのグループにも含まれていることが表で示されています。同じ文字を共有する平均値間の差は統計的に有意ではありません。配合2と4は同じ文字を共有していないため、配合4の平均は配合2よりも有意に高いことを示しています。
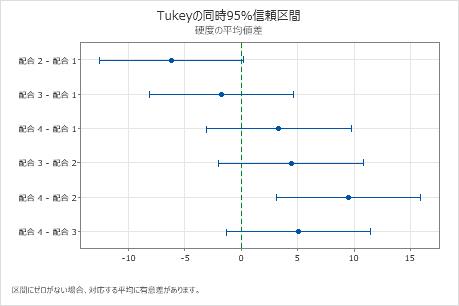
平均の差に対するTukeyの同時検定
| 水準の差 | 平均値差 | 差の標準誤差 | 95%信頼区間 | t値 | 調整されたp値 |
|---|---|---|---|---|---|
| 配合 2 - 配合 1 | -6.17 | 2.28 | (-12.55, 0.22) | -2.70 | 0.061 |
| 配合 3 - 配合 1 | -1.75 | 2.28 | (-8.14, 4.64) | -0.77 | 0.868 |
| 配合 4 - 配合 1 | 3.33 | 2.28 | (-3.05, 9.72) | 1.46 | 0.478 |
| 配合 3 - 配合 2 | 4.42 | 2.28 | (-1.97, 10.80) | 1.94 | 0.245 |
| 配合 4 - 配合 2 | 9.50 | 2.28 | (3.11, 15.89) | 4.17 | 0.002 |
| 配合 4 - 配合 3 | 5.08 | 2.28 | (-1.30, 11.47) | 2.23 | 0.150 |
主要な結果:95%の同時信頼区間、個別信頼水準
- 配合2と配合4の平均値差の信頼区間は、3.11から15.89の範囲にあります。この範囲には0が含まれていないため、これらの平均値差は統計的に有意です。
- 残りの平均ペアの信頼区間にはすべて0が含まれていますが、これは平均値差が統計的に有意ではないことを示しています。
- 95%の同時信頼水準では、全ての信頼区間に真の差が含まれるということを95%信頼できます。
- この表は、個別信頼水準が98.89%であることを示しています。この結果は、各個別区間は特定のグループペア平均の真の差を含んでいるということを98.89%信頼できることを示しています。各比較に対する個別信頼水準から6つの比較全てに対して95%の同時信頼水準が得られます。
ステップ4: データに対するモデルの適合度を判断する
データに対するモデルの適合度を判断するために、モデル要約表の適合度統計量を調査します。
- S
- Sを使い、モデルがどの程度良好に応答を表示するか判断します。
Sは応答変数の単位で測定され、データ値と適合値の間の距離を表します。Sの値が小さければ小さいほど、モデルによる応答の記述が良好になります。ただし、Sの値が小さいだけでは、そのモデルが仮定を満たしているとは言い切れません。残差プロットを確認して仮定を検証する必要があります。
- R二乗
-
R2は、モデルで説明される応答の変動のパーセントです。R2値が大きくなるほど、モデルのデータへの適合度は上がります。R2は常に0~100%の間の値になります。
R2値が大きくても、そのモデルが仮定を満たしているとは言い切れません。残差プロットを確認して仮定を検証する必要があります。
- R二乗(予測)
-
予測R2を使用して、モデルが新しい観測値に対する応答をどの程度良好に予測するかを判断します。予測R2値が大きいモデルの予測能力は優れています。
R2よりも大幅に低い予測R2は、モデルの過剰適合を示している可能性があります。過剰適合は、母集団には重要でない項を追加した場合に起こります。そのモデルはサンプルデータに即してしまい、母集団の予測に適さなくなる可能性があります。
予測R2は、モデル計算に含まれていない観測値によって計算されるため、モデルを比較する場合は調整済みR2より便利です。
モデル要約
| S | R二乗 | R二乗 (調整済み) | R二乗 (予測) |
|---|---|---|---|
| 3.95012 | 47.44% | 39.56% | 24.32% |
主要な結果:S、R二乗、R二乗(予測)
この結果では、因子は応答における47.44%の変動を説明しています。Sはデータ点と適合値間の標準偏差がおよそ3.95個であることを示しています。
ステップ5:モデルが分析の仮説を満たすかどうか判断する
残差プロットを使用して、モデルが適切か、分析の仮定が満たされているかどうかを判断しやすくします。仮定を満たさない場合、そのモデルはデータにあまり適合しない可能性があり、結果の解釈は慎重に行う必要があります。
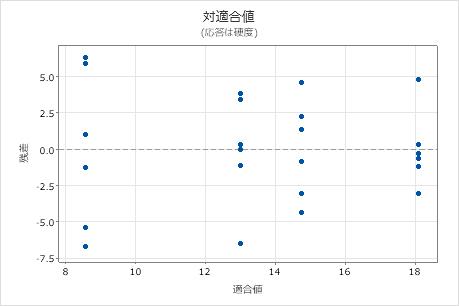
残差対適合値プロット
残差対適合値プロットを使用して、残差はランダムに分布し、均一な分散が存在するという仮定を検証します。点に特徴的なパターンがなく、0の両側にランダムにくるのが理想的です。
| パターン | パターンが示す意味 |
|---|---|
| 残差が適合値周辺に扇状または不均等に分散している | 不均一分散 |
| ゼロから遠い点 | 外れ値 |
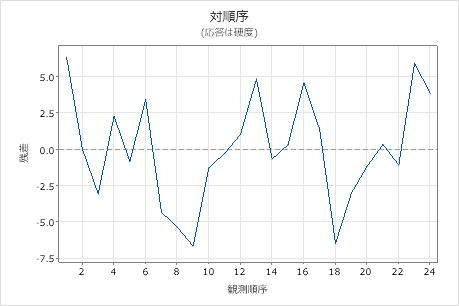
残差対順序プロット
トレンド
シフト
周期
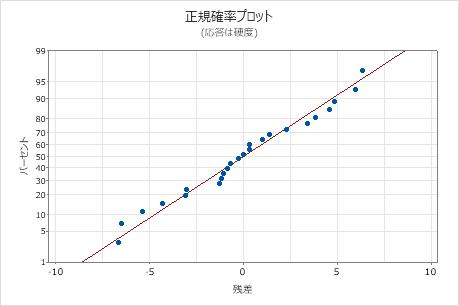
残差の正規確率プロット
残差の正規確率プロットを使用して、残差が正規分布に従うという仮定を検証します。残差の正規確率プロットは、ほぼ直線になります。
| パターン | パターンが示す意味 |
|---|---|
| 直線ではない | 非正規性 |
| 直線から離れた点 | 外れ値 |
| 変化する傾き | 未確認の変数 |
注
一元配置分散分析の計画がサンプルサイズのガイドラインに従っている場合、得られる結果は正規性からの逸脱には大きく影響されません。