N
サンプルサイズ(N)は、各グループに含まれる観測値の合計数です。
解釈
サンプルサイズは信頼区間と検出力に影響します。
通常、サンプルが大きいと信頼区間は狭くなり、差の検出力も高くなります。
平均
各グループにおける観測値の平均です。平均とはデータの中心値を確認できる単一の値で、各グループを表しています。各グループを示す単一の値です。これはグループのすべての観測値の和をそのグループの観測値数で割ったものです。
解釈
各サンプルの平均値は、各母平均の推定値です。サンプルの平均値の差は母平均の差の推定値です。
グループ平均の差は母集団全体ではなくサンプルデータに基づいているため、必ずしも母集団の差に等しいとは言い切れません。母集団の差についてより理解するには、信頼区間を使用してください。
グループ
グループ化情報表を使用し、いずれのグループペアの平均差も統計的に有意であるかどうかを素早く判断します。
グループ列には因子水準をグループ化する文字が含まれています。同じ文字を共有しないグループは統計的に有意な平均差を有しています。
統計的に有意な差が表で特定される場合は、差の信頼区間からその差が実質的に有意であるかどうかを判断します。
解釈
Tukey法と95%信頼水準を使用したグループ化情報
| 塗料 | N | 平均 | グループ化 | |
|---|---|---|---|---|
| 配合 4 | 6 | 18.07 | A | |
| 配合 1 | 6 | 14.73 | A | B |
| 配合 3 | 6 | 12.98 | A | B |
| 配合 2 | 6 | 8.57 | B | |
この結果では、グループAは配合1、3、4を含み、グループBは配合1、2、3を含み、配合1と3はどちらのグループにも含まれていることが表で示されています。同じ文字を共有する平均値間の差は統計的に有意ではありません。配合2と4は同じ文字を共有していないため、配合4の平均は配合2よりも有意に高いことを示しています。
フィッシャーの平均の差の個別検定
個別信頼区間を用いグループ平均差における統計的な有意性の特定、差が含まれる可能性が高い範囲の特定、これらの差が実質的に有意かどうかの判断を行います。平均ペア間における差の信頼区間のセットをフィッシャーの個別検定表に示します。
個別信頼水準とは、分析が2回以上繰り返された場合に、1つの信頼区間に1つのグループペア平均の真の差が含まれる回数の割合のことを言います。個別信頼区間はフィッシャーの方法でのみ利用できます。その他の比較手法では同時信頼区間が得られます。
許容できない水準まで上昇することが多い同時信頼水準を制御できないため、個別信頼水準の制御は一般的ではありません。同時信頼水準を制御しない場合、少なくとも1つの信頼区間に真の差が含まれない確率は、比較の回数に応じて増加します。
差の信頼区間は、次の2つの部分で構成されています。
- 点推定
- 点推定は、平均ペア間の差であり、サンプルデータから算出されます。信頼区間は、この値を中心にして得られます。
- 誤差幅
- 誤差幅は、信頼区間の幅の定義に使用され、サンプルおよび信頼水準における観測された変動性によって決まります。信頼区間の上限を計算するには、誤差幅を点推定に加算します。信頼区間の下限を計算するには、点推定から誤差幅を減算します。
解釈
信頼区間を使用し、グループ平均の差を評価します。
平均の差に対するFisherの個別検定
| 水準の差 | 平均値差 | 差の標準誤差 | 95%信頼区間 | t値 | 調整されたp値 |
|---|---|---|---|---|---|
| 配合 2 - 配合 1 | -6.17 | 2.28 | (-10.92, -1.41) | -2.70 | 0.014 |
| 配合 3 - 配合 1 | -1.75 | 2.28 | (-6.51, 3.01) | -0.77 | 0.452 |
| 配合 4 - 配合 1 | 3.33 | 2.28 | (-1.42, 8.09) | 1.46 | 0.159 |
| 配合 3 - 配合 2 | 4.42 | 2.28 | (-0.34, 9.17) | 1.94 | 0.067 |
| 配合 4 - 配合 2 | 9.50 | 2.28 | (4.74, 14.26) | 4.17 | 0.000 |
| 配合 4 - 配合 3 | 5.08 | 2.28 | (0.33, 9.84) | 2.23 | 0.037 |
- 配合2と配合4の平均値差の信頼区間は、4.74から14.26の範囲にあります。この範囲には0が含まれていないため、これらの平均値差は統計的に有意です。
- 配合2と配合1の平均値差の信頼区間は、-10.92から-1.41の範囲にあります。この範囲には0が含まれていないため、これらの平均値差は統計的に有意です。
- 配合4と配合3の平均値差の信頼区間は、0.33から9.84の範囲にあります。この範囲には0が含まれていないため、これらの平均値差は統計的に有意です。
- 残りの平均ペアの信頼区間にはすべて0が含まれているため、これらの平均値差は統計的に有意ではありません。
- 95%の個別信頼水準は、各信頼区間に特定の比較における真の差が含まれているということを95%信頼できます。ただし、同時信頼水準の場合、全ての区間に真の差が含まれる信頼度は80.83%です。
平均値差
2つのグループのサンプル平均間の差です。
解釈
グループ間のサンプル平均値の差は、これらのグループにおける母集団の差の推定値です。
各平均差は母集団全体ではなくサンプルからのデータに基づいているため、母集団の差に等しいとは限りません。母平均間の差をよく理解するために、信頼区間を使用します。
差の標準誤差
平均値間の標準誤差(差の標準誤差)は、同じ母集団からサンプル採取を繰り返し行った場合に得られる、サンプルの平均値間に見られる変動性を推定します。
解釈
平均値間の標準誤差から、サンプル平均値の差によって推定される母平均の差の正確さを判定します。標準誤差値が低いほど推定が正確であることを示しています。
Minitabは差の標準誤差から、母数差が含まれる可能性が高い範囲となる、平均値間の差の信頼区間を算出します。
95%の信頼区間(CI)
差の同時信頼区間(95%の信頼区間)を使用して、統計的に有意な平均差を特定し、差の値が含まれそうな範囲を決定し、差の実際的な有意性を評価します。表は、平均ペア間の差の信頼区間の一組を示しています。0を含まない信頼区間は、統計的に有意な平均差を示しています。
同時信頼水準とは、調査を複数回繰り返した場合に、一組の信頼区間がすべてのグループ比較の真の差を含んでいる回数の割合のことです。
同時信頼水準を制御することは、多重比較を実行する場合に特に重要です。同時信頼水準を制御しない場合、少なくとも1つの信頼区間に真の差が含まれない確率は、比較の回数に応じて増加します。
差の信頼区間は、次の2つの部分で構成されています。
- 点推定
- 点推定は、平均ペア間の差であり、サンプルデータから算出されます。信頼区間は、この値を中心にして得られます。
- 誤差幅
- 誤差幅は、信頼区間の幅を定義し、サンプル、サンプルサイズ、信頼水準において観測された変動性によって決定します。信頼区間の上限を計算するには、誤差幅を点推定に加算します。信頼区間の下限を計算するには、点推定から誤差幅を減算します。全ての区間が真の母数差を含むという同時信頼水準を維持するため、誤差幅は比較の回数に応じて拡大します。
解釈
信頼区間を使用し、グループ平均の差を評価します。
平均の差に対するTukeyの同時検定
| 水準の差 | 平均値差 | 差の標準誤差 | 95%信頼区間 | t値 | 調整されたp値 |
|---|---|---|---|---|---|
| 配合 2 - 配合 1 | -6.17 | 2.28 | (-12.55, 0.22) | -2.70 | 0.061 |
| 配合 3 - 配合 1 | -1.75 | 2.28 | (-8.14, 4.64) | -0.77 | 0.868 |
| 配合 4 - 配合 1 | 3.33 | 2.28 | (-3.05, 9.72) | 1.46 | 0.478 |
| 配合 3 - 配合 2 | 4.42 | 2.28 | (-1.97, 10.80) | 1.94 | 0.245 |
| 配合 4 - 配合 2 | 9.50 | 2.28 | (3.11, 15.89) | 4.17 | 0.002 |
| 配合 4 - 配合 3 | 5.08 | 2.28 | (-1.30, 11.47) | 2.23 | 0.150 |
- 配合2と配合4の平均値差の信頼区間は、3.11から15.89の範囲にあります。この範囲には0が含まれていないため、これらの平均値差は統計的に有意です。
- 残りの平均ペアの信頼区間にはすべて0が含まれていますが、これは平均値差が統計的に有意ではないことを示しています。
- 95%の同時信頼水準とは、これら全ての信頼区間に真の差が含まれるということを95%信頼できるということです。
- 98.89%の個別信頼水準とは、各信頼区間において、その特定の比較についての真の差が含まれていることを、98.89%信頼できることを示しています。
t値
t値は、平均差と差の標準誤差の比を測定する検定統計量です。
解釈
t値を使用して、平均差は0であるとする帰無仮説を棄却するか否かを判断することができますが、一般的には解釈がより容易なp値が使われます。棄却限界値に関する詳細については、t値を使用して、帰無仮説を棄却するかどうかを判断するを参照してください。
t値を使ってp値を算出します。
調整されたp値
調整されたp値は、全体比較のうちどのペアが有意に異なるかを示します。この調整により全体過誤率を指定したα水準に制限します。多重比較で通常のp値を使用すると、全体過誤率は比較を追加するたびに増加します。
多重比較を行う際は、全体過誤率を考慮することが重要です。一連の比較における第1種の過誤の確率は、1つの比較の過誤率よりも高くなるためです。
解釈
調整されたp値がαより小さい場合は、帰無仮説を棄却しグループペア平均の差が統計的に有意であると結論付けます。また、調整されたp値は、特定の帰無仮説を棄却する最小全体過誤率を表します。
平均の差の区間プロット
差が含まれる可能性が高い範囲を特定し、これらの差の実質的な有意性を評価するためい信頼区間を使用します。平均ペア間における差の信頼区間のセットをグラフに示します。0が含まれていない信頼区間は、統計的に有意な平均差であることを示しています。
選択した比較手法によって、プロットは異なるグループペアを比較し以下のいずれかの信頼区間を表示します。
-
個別信頼水準
分析が2回以上繰り返された場合に、1つの信頼区間に1つのグループペア平均の真の差が含まれる回数の割合
-
同時信頼水準
分析が2回以上繰り返された場合に、信頼区間のセットにすべてのグループ比較の真の差が含まれる回数の割合
同時信頼水準の管理は、複数の比較を実行する場合に特に重要です。同時信頼水準を管理しない場合、少なくとも1つの信頼区間に真の差が含まれない確率は、比較の回数に応じて増加します。
解釈
- 配合4と配合2の平均値差の信頼区間は、3.11から15.89の範囲にあります。この範囲には0が含まれていないため、これらの平均値差は統計的に有意であることを示しています。
- 残りの平均ペアの信頼区間にはすべて0が含まれているため、これらの平均値差は統計的に有意ではありません。
- 95%同時信頼水準では、これら全ての信頼区間に真の差が含まれるということを95%信頼できます。
- 各個別信頼区間は98.89%の信頼度を有します。この結果から、各個別区間は特定のグループペア平均の真の差を含んでいることを98.89%信頼できることになります。各比較に対する個別信頼水準から6つの比較全てに対して95%の同時信頼水準が得られます。
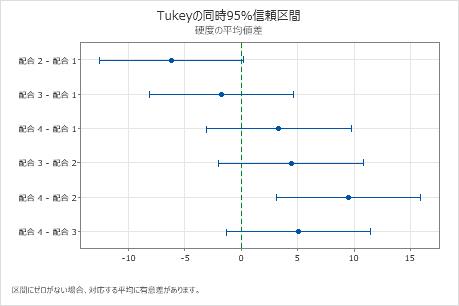
平均の差に対するTukeyの同時検定
| 水準の差 | 平均値差 | 差の標準誤差 | 95%信頼区間 | t値 | 調整されたp値 |
|---|---|---|---|---|---|
| 配合 2 - 配合 1 | -6.17 | 2.28 | (-12.55, 0.22) | -2.70 | 0.061 |
| 配合 3 - 配合 1 | -1.75 | 2.28 | (-8.14, 4.64) | -0.77 | 0.868 |
| 配合 4 - 配合 1 | 3.33 | 2.28 | (-3.05, 9.72) | 1.46 | 0.478 |
| 配合 3 - 配合 2 | 4.42 | 2.28 | (-1.97, 10.80) | 1.94 | 0.245 |
| 配合 4 - 配合 2 | 9.50 | 2.28 | (3.11, 15.89) | 4.17 | 0.002 |
| 配合 4 - 配合 3 | 5.08 | 2.28 | (-1.30, 11.47) | 2.23 | 0.150 |
