箱ひげ図
箱ひげ図では各サンプル分布のグラフ要約を表示します。箱ひげ図を使用すると、サンプル分布の形、中心傾向、変動性の比較が容易になります。
解釈
箱ひげ図を使用して、データの広がりを調べ、潜在的な外れ値を確認します。箱ひげ図は、サンプルサイズが20より大きい場合に最適です。
- 歪んだデータ
-
データの広がりを調べ、データが歪んでいるかどうかを判断します。データが歪んでいる場合、ほとんどのデータがグラフの上下に位置していることになります。歪んだデータはデータが正規に分布されていない可能性を示唆しています。歪みは、個別値プロット、ヒストグラム、または箱ひげ図によって最も簡単に検出する事ができます。

右方向の歪み

左方向の歪み
右方向に歪んだデータは、平均待ち時間を示します。待ち時間のほとんどは比較的短く、ごく少数の待ち時間だけが長くなります。左方向に歪んだデータは、故障率を示します。少数の項目が直ちに故障し、より多くの項目が後で故障します。
データが大きく歪んでいると、サンプルサイズが小さい場合(20未満)にp値の妥当性が影響を受けます。データが大きく歪んでいて、サンプルサイズが小さい場合はサンプルサイズを増やすことを検討します。
- 外れ値
-
外れ値は、他のデータから遠くに離れているデータ値のことで、分析の結果に大きな影響を及ぼします。多くの場合、外れ値は、箱ひげ図で容易に識別できます。
箱ひげ図では、アスタリスク(*)が外れ値を意味します。
外れ値がある場合は、その原因を特定してください。データ入力誤差や測定誤差はすべて修正します。異常な1回だけの事象(特殊原因)を示すデータ値を除外することを検討してください。それから、分析を繰り返します。
個別値プロット
個別値プロットは各サンプルに対して個別の値を表示します。個別値プロットではサンプル同士の比較が容易に行えます。各円は1つの観測値を表しています。個別値プロットは、サンプルサイズが小さい場合には特に有益です。
解釈
個別値プロットを使用して、データの広がりを調べ、潜在的な外れ値を識別します。個別値プロットは、サンプルサイズが50未満の場合に最適です。
- 歪んだデータ
-
データの広がりを検討し、データが歪んでいるかどうかを判断します。データが歪んでいる場合、ほとんどのデータがグラフの上下に位置していることになります。歪んだデータはデータが正規に分布されていない可能性を示唆しています。歪みは、個別値プロット、ヒストグラム、または箱ひげ図によって最も簡単に検出する事ができます。
右方向の歪み
左方向の歪み
右方向に歪んだデータのある個別値プロットは、待ち時間を示します。待ち時間のほとんどは比較的短く、ごく少数の待ち時間だけが長くなります。左方向に歪んだデータのある個別値プロットは、故障寿命を示します。少数の項目が直ちに故障し、もっと多くの項目が後で故障します。
- 外れ値
-
外れ値は、他の大部分のデータから離れているデータ値のことで、分析の結果に大きな影響を及ぼします。多くの場合、外れ値は個別値プロットで容易に識別できます。
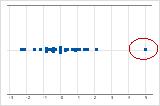
個別値プロットでは、異常に低いか、または高いデータ値によって、潜在的な外れ値が示されます。
外れ値がある場合は、その原因を特定してください。データ入力誤差や測定誤差はすべて修正します。異常な1回だけの事象(特殊原因)を示すデータ値の除外を検討してください。その後分析を繰り返します。
区間プロット
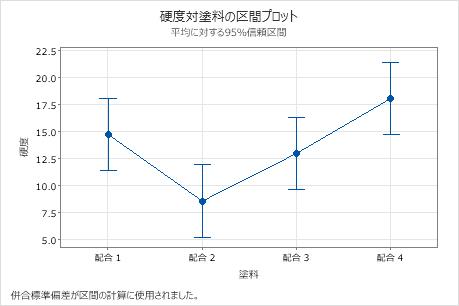
区間プロットを使用して、各グループの平均値と信頼区間を表示します。
- ドットはサンプル平均を示します。
- 各区間はグループ平均の95%の個別信頼区間です。グループ平均がそのグループの信頼区間に含まれることを95%信頼できます。
重要
多重比較を行うことにより第1種過誤率が増加するため、各区間の解釈は慎重に行ってください。つまり比較回数が増加するにつれて、少なくとも1つの比較結果において、観測された差が有意に異なっているという間違って結論付けられる可能性が高まるためです。
解釈
この結果では、配合2の平均が最低であり、配合4の平均が最高であることがわかります。このグラフからは、いずれの差についても、統計的に有意であるかどうかは判断できません。統計的な有意性を判断するには、平均の差の信頼区間を評価します。