目的の方法または計算式を選択してください。
分散成分
パラメータθiを推定するためには、分散分析に繰り返し解が必要です。パラメータを得たら、分散成分には明白な解が与えられます。誤差の分散成分を求める計算式は以下になります。
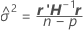

ここで、
以下は変量効果項の分散成分です。


θiの推定に関する詳細は(1)を参照してください。
表記に関する詳細は、「方法」のセクションを参照してください。
参考文献
- Hemmerle, W. and Hartley, H. (1973). Computing Maximum Likelihood Estimates for the Mixed A.O.V. Model using the W transformation. Technometrics, 15(4):819–831頁.
分散成分の標準誤差
分散成分の標準誤差を推定するために、観測フィッシャー情報行列から開始します。行列にはc + 1の行と列があります。変数cは、モデルに含まれるランダム効果項の数で、1は誤差項の分散を表します。i = 1, …, c、およびj = 1, …, cにおいて、観測フィッシャー情報行列のij番目の成分の計算式は以下になります。
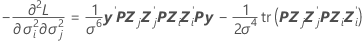
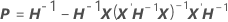
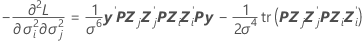
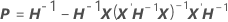
以下の計算式は最終行および 列、j = 1, …, cの成分です。
列、j = 1, …, cの成分です。
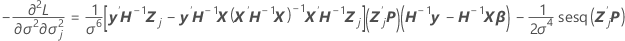

 列、j = 1, …, cの成分です。
列、j = 1, …, cの成分です。
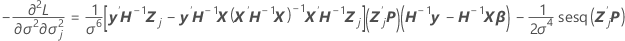

この成分はまた、最終列および 行の値です(分散共分散行列の対称性)。
行の値です(分散共分散行列の対称性)。
以下の計算式は最終行および最終列の成分です。


分散成分の推定値の漸近的な分散共分散行列は、観測フィッシャー情報行列の逆行列を2倍にしたものです。標準誤差の推定値は、分散共分散行列の対角要素の平方根です。最初のc対角要素は変量効果項の分散成分の要素です。最後の対角要素は、誤差分散成分の要素です。
表記
| 用語 | 説明 |
|---|---|
 | 行列の追跡 |
 | 行列Mに含まれるすべての要素の平方和 |
表記に関する詳細は、「方法」のセクションを参照してください。
分散成分の信頼区間
Minitabはデルタ法を使用して、分散成分の自然対数ワルドタイプの信頼限界を構成し、信頼区間をべき乗して分散成分の信頼区間を導き出します。誤差の分散成分を求める計算式も同じ形を取ります。
両側区間
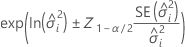
下限
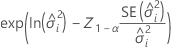
上限
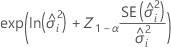
表記
| 用語 | 説明 |
|---|---|
 | 管理図の中でも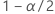 百分位(標準正規分布から得られる) 百分位(標準正規分布から得られる) |
 | 1 − 信頼水準 |
 | 分散成分の標準誤差( 分散成分) 分散成分) |
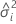 | ランダム効果項の分散成分( ランダム効果項) ランダム効果項) |
Z値とp値
この検定では、帰無仮説と対立仮説は次のようになります。
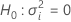
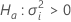
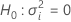
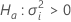
検定統計量は以下のような標準正規分布の仮説を立てます。


p値は帰無仮説の下で、標準正規分布に基づく以下のような右肩あがりの確率です。


表記
| 用語 | 説明 |
|---|---|
| Z | 標準正規分布の逆累積分布関数の値 |
分散共分散行列
漸近的な分散共分散行列は、観測フィッシャー情報行列を逆行列にしたものです。行列にはc + 1の行と列があります。変数cは、モデルに含まれるランダム効果項の数で、1は誤差項の分散を表します。i = 1, …, cおよびj = 1, …, cにおいて、観測フィッシャー情報行列の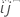 成分の計算式は以下になります。
成分の計算式は以下になります。
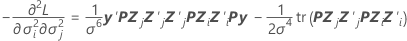

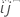 成分の計算式は以下になります。
成分の計算式は以下になります。
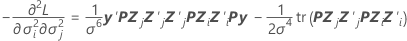

以下の計算式は最終行および 列、j = 1, …, cの成分です。
列、j = 1, …, cの成分です。
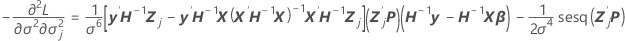

 列、j = 1, …, cの成分です。
列、j = 1, …, cの成分です。
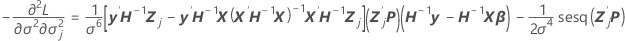

この成分はまた、最終行および 行の値です(分散共分散行列の対称性)。
行の値です(分散共分散行列の対称性)。
以下の計算式は最終行および最終列の成分です。


表記
| 用語 | 説明 |
|---|---|
 | 行列の追跡 |
表記に関する詳細は、「方法」のセクションを参照してください。
