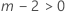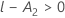固定効果項の検定
固定効果項の検定はF検定です。検定の帰無仮説は、固定効果項を使う検定なのか共変量項を使った検定なのかによって異なります。固定因子項の場合、帰無仮説は項が応答に大きく影響しないという仮定です。共変量項の場合の帰無仮説は、応答と共変量項に関連性がないという仮定です。
Minitabでの固定効果項の検定には、ケンワードｰロジャー（Kenward-Roger）の近似とサタスウェイト（Satterthwaite）の近似の2種類が利用できます。ケンワードｰロジャーの近似に関する詳細は、『Kenward and Roger.1』を参照してください。サタスウェイトの近似に関する詳細は、『Giesbrecht and Burns 2』および『Fai and Cornelius. 3』を参照してください。
F統計量の分母の自由度の計算と、F統計量の計算は異なります。分子の自由度の計算と、与えられたF統計量に対するp値の決定はどちらの方法でも共通です。
ケンワードｰロジャー（Kenward-Roger）の近似
ケンワードｰロジャー（Kenward-Roger）の近似は固定効果項の統計的有意性を検定する一つの手法です。
F統計量
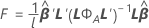
ここで
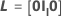
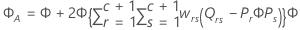
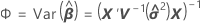
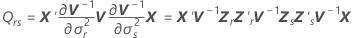
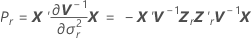
表記
| 用語 | 説明 |
|---|---|
| l | 検定する項に含まれるパラメータ数である分子自由度 |
| 0 | 成分が0個の行列 |
| Il | l次元を持つ恒等行列 |
| c + 1 | 分散成分の数 |
| wrs | の漸近的な分散共分散行列の(r, s)番目の成分。  |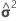
| V−1 | 分散共分散行列の逆行列 |
表記に関する詳細は、「方法」のセクションを参照してください。
分母自由度
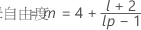
ここで
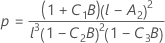
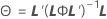
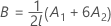
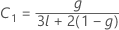
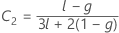
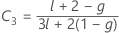
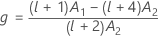
ケンワードｰロジャー（Kenward-Roger）のλ
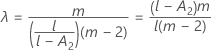
いずれかの条件が真でない場合、λ = 1になります。
帰無仮説の下では、λ × Fは分子自由度（DF Num）と分母自由度（DF Den）の自由度で漸近的にＦ分布に従います。p値の計算にはこの特性が使用されます。
サタスウェイト（Satterthwaite）の近似
サタスウェイト（Satterthwaite）の近似は固定効果項の統計的有意性を検定する一つの手法です。
F 統計量
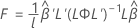
ここでLと
の定義はケンワードｰロジャー（Kenward-Roger）の近似と同じです。
分母自由度
自由度を決定する工程には、段階が複数あります。
-
固定効果パラメータのベクトル推定値の分散に対してスペクトル分解を実行します。
ここでPは固有ベクトルの直交行列、Dは固定値の対角行列で、次元は共にl × lです。
-
lrがP'L,r = 1, ..., lのr番目の行となるように定義し、
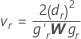ここでdrはDの r番目の対角要素で、Wは
の漸近的な分散共分散行列、そしてgrは次の要素の勾配ベクトルです。
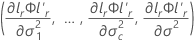
ここで、
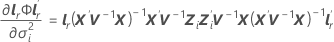
i = 1, …, c、及び
-
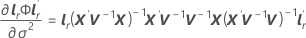
次のように定義します。
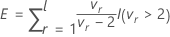
ここで、
は項を取り除く指示関数です。項：
-
分母の自由度はEの値により異なります。
- E > lの場合、自由度は以下の式に従います。
- それ以外の場合は分母自由度 = 1です。
- E > lの場合、自由度は以下の式に従います。
分子の自由度（DF Num）
| 効果 | 自由度（DF） |
|---|---|
| 固定因子 |  |
| 共変量 | 1 |
| 固定因子を含む交互作用 |  |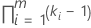
表記
| 用語 | 説明 |
|---|---|
| k | 固定因子項の水準数 |
| m | 交互作用の因子数 |
p値～固定効果の検定
表記
| 用語 | 説明 |
|---|---|
 | 自由度がDF NumとDF Denにそれぞれ等しいF分布の累積分布関数 |
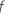 | 項に対して計算されたF値 |
