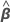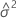目的の方法または計算式を選択してください。
このトピックの内容
混合効果モデルと対数尤度
混合効果モデルの一般形
混合効果モデルには、固定効果とランダム効果の両方が含まれます。混合効果モデルの一般形は以下になります。
y = Xβ + Z1μ1+ Z2μ2 + ... + Zcμc + ε
表記
| 用語 | 説明 |
|---|---|
| y | 応答値のn x 1ベクトル |
| X | 固定効果項がp ≤ nの場合のn x p計画行列 |
| β | 未知のパラメータのp x 1ベクトル |
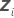 | n x mi計画行列はモデル内の ランダム項に対応 ランダム項に対応 |
| μi | 次から得られる独立変数のmi x 1ベクトル:N(0, ) ) |
| ε | 次から得られる独立変数のn x 1ベクトル:N(0,  ) ) |
| n | 観測値数 |
| p | パラメータ数 |
| c | モデル内のランダム項の数 |
分散共分散行列
混合効果モデルの一般形のモデルの仮定に基づき、応答ベクトルyは、平均ベクトルXβの多変量正規分布となり、次の分散共分散行列を持ちます。
V(σ2) = V(σ2, σ21, ... , σ2c) = σ2In + σ21Z1Z'1 + ... + σ2cZcZ'c
ここで
σ2 = (σ2, σ21, ... , σ2c)'
σ2, σ21, ... , σ2cは分散成分と呼ばれます。
分散から因数分解することで、混合効果モデルの対数尤度の計算部分にあるH(θ)の表現を見つけることができます。
V(σ2) = σ2H(θ) = σ2[In + θ1Z1Z'1 + ... + θcZcZ'c]
表記
| 用語 | 説明 |
|---|---|
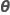 | 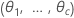 |
| θi | 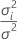 誤差分散内の 誤差分散内の ランダム項の分散の比率 ランダム項の分散の比率 |
対数尤度
モデルに変量因子が含まれる場合、未知のパラメータ推定値はデフォルトで、制限された対数尤度関数の負の値を2倍したものを最小化することで発生します。最小化は、制限された対数尤度関数の最大化と同じです。Minitabでは反復アルゴリズムを使って制限された対数尤度関数が最小化されます。最小化する関数は以下になります。




表記
| 用語 | 説明 |
|---|---|
| H | In + θ1Z1Z'1 + ... + θcZcZ'c |
| |H| | Hの行列式 |
| H-1 | Hの逆行列 |
| mi |  ランダム項の水準数 ランダム項の水準数 |
 | 誤差の分散成分 |
| In | nの行と列を持つ恒等行列 |
制限付き最尤法(REML)の推定
デフォルトでは、制限付き尤度関数を最大にするパラメータ推定値が計算されますが、これは次の関数を最小にするのと同等です。
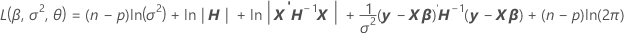
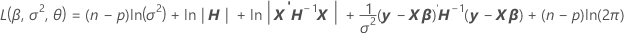
関数を最小にするために、β、σ2、およびθiで関数が識別され、差分が0に設定されます。
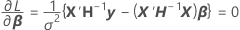
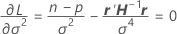
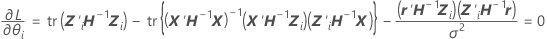
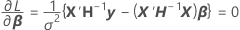
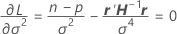
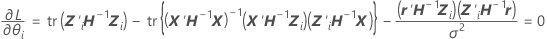
ここで、
識別に関してパラメータ推定値を求めるために最初の2つの等式で代数を再配列すると、以下の等式になります。
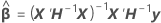
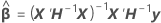

導関数で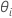 に関しては
に関しては 。Minitabではニュートン法により
。Minitabではニュートン法により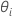 の推定が以下の手順で行なわれます。
の推定が以下の手順で行なわれます。
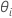 に関しては
に関しては 。Minitabではニュートン法により
。Minitabではニュートン法により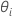 の推定が以下の手順で行なわれます。
の推定が以下の手順で行なわれます。
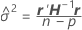
収束した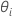 の解は分散比の推定値です。このとき
の解は分散比の推定値です。このとき ランダム項の分散成分は以下になります。
ランダム項の分散成分は以下になります。

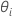 の解は分散比の推定値です。このとき
の解は分散比の推定値です。このとき ランダム項の分散成分は以下になります。
ランダム項の分散成分は以下になります。

表記
| 用語 | 説明 |
|---|---|
| tr(·) | 行列の跡 |
| X' | Xの転置 |
1 Rao, C.R. (1971 a). Estimation of variance covariance components - MINQUE theory. Journal of Multivariate Analysis 1, 257–275.
2 Rao, C.R. (1971 b). 分Minimum variance quadratic unbiased estimation of variance components. Journal of Multivariate Analysis 1, 445–456.