ある研究者がランダムに選択した4つの畑における6品種のアルファルファの生産高を分析します。各畑の各品種の収量が記録されました。
研究者は、アルファルファの品種が平均収穫量に影響するかどうかを調べようとしています。データを収集できる対象の畑は4つあります。しかし、研究者は実験対象外の畑におけるアルファルファの生長をモデル化できるようにしたいと考えています。このため、研究者はアルファルファの生育地を変量因子にしました。研究者は混合効果モデルを使用して固定効果とランダム効果を同時に評価します。
- サンプルデータを開くアルファルファ.MWX.
- を選択します。
- 応答に生産高を入力します。
- 変量因子(必須)に畑を入力します。
- 固定因子に品種を入力します。
- グラフをクリックします。
- プロットの残差で、 条件付き、標準化を選択します。
- 残差プロットで、 一覧表示を選択します。
- 各ダイアログでOKをクリックします。
結果を解釈する
分散成分表において、「畑」のp値は0.124です。仮説検定では、分散成分が0と異なるという証拠は示されません。誤差の分散成分のp値は0.003です。p値は有意水準0.05よりも小さいため、研究者は誤差の分散成分が0ではないと結論付けることができます。
固定因子項「品種」のおよそ0のp値は、少なくとも1品種のアルファルファが収穫量に与える影響が、他の5品種と有意に異なることを示しています。
主効果の係数は各水準毎の平均と全体平均の差を表します。たとえば、「品種1」の収穫量は全体平均よりおよそ0.385単位大きくなっています。この係数に対するおよそ0のp値は、「品種1」が収穫量に与える影響が「品種」項の他の水準効果と有意に異なることを示しています。どの水準効果が統計的に同じで、どの水準効果が統計的に異なるかを判断するために、研究者は項の多重比較分析を行うことにしました。
R2値は、モデルによって92%の収穫量の変動が説明されることを示しています。R二乗(調整済み)の値もおよそ90.2%と高くなっています。研究者はこの値を使用して、予測変数の数が異なるモデルを比較します。
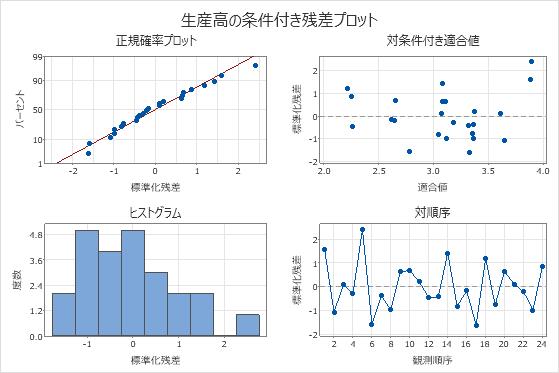
観測値1と5の標準化残差は2より大きいため、異常な観測値です。研究者はデータを調査して、これらの観測値の応答値が正しいことを確認します。
正規確率プロットの残差はほぼ直線上に分布し、残差対適合値プロット上では0の周囲にランダムに散在しているように見えます。
方法
| 分散推定 | 制約型最尤法 |
|---|---|
| 固定効果のDF | Kenward-Roger |
因子情報
| 因子 | タイプ | 水準 | 値 |
|---|---|---|---|
| 畑 | ランダム | 4 | 1, 2, 3, 4 |
| 品種 | 固定 | 6 | 1, 2, 3, 4, 5, 6 |
分散成分
| 要因 | 分散 | 合計の% | 標準偏差の分散 | Z-値 | p値 |
|---|---|---|---|---|---|
| 畑 | 0.077919 | 72.93% | 0.067580 | 1.152996 | 0.124 |
| 誤差 | 0.028924 | 27.07% | 0.010562 | 2.738613 | 0.003 |
| 合計 | 0.106843 |
固定効果の検定
| 項 | DF 分子 | DF 分母 | F値 | p値 |
|---|---|---|---|---|
| 品種 | 5.00 | 15.00 | 26.29 | 0.000 |
モデル要約
| S | R二乗 | R二乗 (調整済み) | AICc(修正済み 赤池情報量基準) | BIC(ベイズ 情報量基準) |
|---|---|---|---|---|
| 0.170071 | 92.33% | 90.20% | 12.54 | 13.52 |
係数
| 項 | 係数 | 係数の標準誤差 | 自由度 | t値 | p値 |
|---|---|---|---|---|---|
| 定数 | 3.094583 | 0.143822 | 3.00 | 21.516692 | 0.000 |
| 品種 | |||||
| 1 | 0.385417 | 0.077626 | 15.00 | 4.965016 | 0.000 |
| 2 | 0.145417 | 0.077626 | 15.00 | 1.873287 | 0.081 |
| 3 | 0.107917 | 0.077626 | 15.00 | 1.390205 | 0.185 |
| 4 | -0.319583 | 0.077626 | 15.00 | -4.116938 | 0.001 |
| 5 | 0.395417 | 0.077626 | 15.00 | 5.093838 | 0.000 |
異常な観測値の周辺適合値と診断
| 観測値 | 生産高 | 適合値 | 残差 | 標準化残差 | |
|---|---|---|---|---|---|
| 1 | 4.100000 | 3.480000 | 0.620000 | 2.190221 | R |
| 5 | 4.220000 | 3.490000 | 0.730000 | 2.578808 | R |
異常な観測値の条件付き適合値と診断
| 観測値 | 生産高 | 適合値 | 残差 | 標準化残差 | |
|---|---|---|---|---|---|
| 5 | 4.220000 | 3.895339 | 0.324661 | 2.400733 | R |