このトピックの内容
ウィルクの検定
検定の統計量、ウィルクのλは、
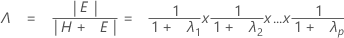
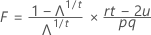
で、pqと(rt – 2u)は自由度です。
表記
| 用語 | 説明 |
|---|---|
| H | 仮説行列 |
| E | 誤差行列 |
| p | 応答数 |
| q | 仮説の自由度 |
| v | Eの自由度 |
| s | min (p, q) |
| m | .5 ( | p – q | – 1) |
| n | .5 (v – p – 1) |
| r | v – 0.5 (p – q + 1) |
| u | 0.25(pq – 2) |
| t | = Sqrt ([p2 q2 - 4] / p2 + q2 - 5(p2 + q2 - 5 > 0の場合) |
| t | 1 |
λ1≥λ2≥λ3≥ . . . ≥λpが(E** - 1) * Hの固有値とします 最初の3つの検定統計量は、HとE、あるいはこれらの固有値のいずれかの形式で表記することができます。
H行列は平方和「間」を各p変数の対角要素に含むp×pの行列です。H行列は次のように計算されます。

E行列は平方和「内」を各p変数の対角要素に含むp×pの行列です。E行列は次のように計算されます。
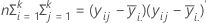
最初の3つの検定で、F-統計量はs = 1または2のときは正確ですが、そうでない場合は近似値となります。検定が近似値の場合はその旨が示されます。
ローリー・ホートリングの検定
検定統計量、ローリー・ホートリングのトレース基準は、

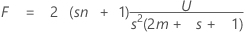
で、s (2m + s + 1)と2 (sn + 1)は自由度です。
表記
| 用語 | 説明 |
|---|---|
| H | 仮説行列 |
| E | 誤差行列 |
| p | 応答数 |
| q | 仮説の自由度 |
| v | Eの自由度 |
| s | min (p, q) |
| m | .5 ( | p – q | – 1) |
| n | .5 (v – p – 1) |
| r | v – 0.5 (p – q + 1) |
| u | 0.25(pq – 2) |
| t | = Sqrt ([p2 q2 - 4] / p2 + q2 - 5(p2 + q2 - 5 > 0の場合) |
| t | 1 |
λ1≥λ2≥λ3≥ . . . ≥λpは(E** - 1) * Hの固有値です。最初の3つの検定統計量は、HとE、あるいはこれらの固有値のいずれかの形式で表記することができます。
H行列は平方和「間」を各p変数の対角要素に含むp×pの行列です。H行列は次のように計算されます。

E行列は平方和「内」を各p変数の対角要素に含むp×pの行列です。E行列は次のように計算されます。
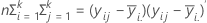
最初の3つの検定で、F-統計量はs = 1または2のときは正確ですが、そうでない場合は近似値となります。検定が近似値の場合はその旨が示されます。
ピライの検定
検定統計量、ピライのトレースは、

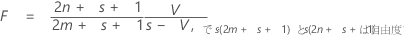
表記
| 用語 | 説明 |
|---|---|
| H | 仮説行列 |
| E | 誤差行列 |
| p | 応答数 |
| q | 仮説の自由度 |
| v | Eの自由度 |
| s | min (p, q) |
| m | .5 ( | p – q | – 1) |
| n | .5 (v – p – 1) |
| r | v – 0.5 (p – q + 1) |
| u | 0.25(pq – 2) |
| t | = Sqrt ([p2 q2 - 4] / p2 + q2 - 5(p2 + q2 - 5 > 0の場合) |
| t | 1 |
λ1≥λ2≥λ3≥ . . . ≥λpは(E** - 1) * Hの固有値です。最初の3つの検定統計量は、HとE、あるいはこれらの固有値のいずれかの形式で表記することができます。
H行列は平方和「間」を各p変数の対角要素に含むp×pの行列です。H行列は次のように計算されます。

E行列は平方和「内」を各p変数の対角要素に含むp×pの行列です。E行列は次のように計算されます。
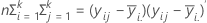
最初の3つの検定で、F-統計量はs = 1または2のときは正確ですが、そうでない場合は近似値となります。検定が近似値の場合はその旨が示されます。
ロイの最大根検定
最大固有値、λ1です。検定を完了させるには、パラメータs、m、nと共にヘック表と呼ばれる特殊な表を使い有意水準を抽出する必要があります。
これらの表については、「ヘック1」を参照してください。
表記
| 用語 | 説明 |
|---|---|
| s | min (p, q) |
| m | .5 ( | p – q | – 1) |
| n | .5 (v – p – 1) |
λ1≥λ2≥λ3≥ . . . ≥λpは(E** - 1) * Hの固有値です。最初の3つの検定統計量は、HとE、あるいはこれらの固有値のいずれかの形式で表記することができます。
- D.L. Heck (1960), "Charts of Some Upper Percentage Points of the Distribution of the Largest Characteristic Root," The Annals of Statistics, 625–642.
