このトピックの内容
適合値
適合値はfitsまたはとも呼ばれます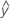
。適合値は、予測変数の値の平均応答の点推定です。予測変数の値はｘ値とも呼ばれます。
解釈
適合値は、データセットに含まれる観測値ごとの特定のx値をモデル式に入力することによって計算されます。
たとえば、式がy = 5 + 10xの場合に、x値が2ならば、適合値は25 (25 = 5 + 10(2))となります。
観測された値と非常に異なる適合値を含む観測値は、異常な観測値である可能性があります。異常な予測値を持つ観測値は、影響力がある可能性があります。Minitabが、データに異常または影響力がある値が含まれていると判断した場合は、これらの観測値が特定された、異常な観測値の適合値と診断の表が出力されます。ラベルが付けられた異常な観測値は、提示された回帰式にしっかりと従っていません。ただし、いくつかの異常な観測値があることは予測されています。たとえば、大きな標準化残差の基準に基づくと、観測値の約5%は大きな標準化残差を持つとしてフラグがつけられることが予測されます。異常な値に関する詳細は、異常な観測値を参照してください。
適合値の標準誤差（SE Fit）
適合値の標準誤差（SE Fit）は、特定の変数設定について推定される平均応答の変動を推定します。平均応答の信頼区間の計算には、適合値の標準誤差が使用されます。標準誤差は常に正数です。この解析では、 統計 メニューのモデルと 予測分析モジュールの 線形回帰 モデルと 2値ロジスティック回帰 モデルの標準誤差が計算されます。
解釈
適合値の標準誤差は、平均応答の推定値の精度を測定するために使用します。標準誤差が小さいほど、予測される平均応答の精度は高くなります。たとえば、分析者が配達時間を予測するモデルを開発するとします。変数設定のひとつのセットに、モデルは3.80日の平均配達時間を予測します。これらの設定の適合値の標準誤差は0.08日です。変数設定の2つめのセットに、モデルは適合値の標準誤差の0.02日で同じ平均配達時間を生成します。分析者は、変数設定の2つめのセットの平均配達時間が3.80日近くであるということに、より自信を持つことができます。
あてはめ値を使用すると、近似の標準誤差を使用して、平均応答の信頼区間を作成できます。たとえば、自由度の数に応じて、95% 信頼区間は、予測平均の上下に約 2 つの標準誤差を拡張します。配達時間の場合、標準誤差が 0.08 の場合の予測平均 3.80 日の 95% 信頼区間は (3.64, 3.96) 日です。これは、95%の信頼度で、母集団の平均がこの範囲に含まれることを意味します。標準誤差が 0.02 の場合、95% 信頼区間は (3.76, 3.84) 日です。変数設定の 2 番目のセットの信頼区間は、標準誤差が小さいため、より狭くなります。
Resid
残差（ei）とは、観測値（y）とそれに対応する適合値（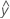
）モデルによって予測される値です。
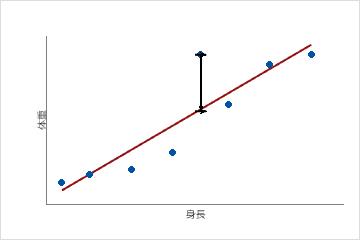
この散布図は成人男性のサンプルの身長対体重を表示しています。適合回帰線は身長と体重の関係を表しています。身長が6フィートであれば、体重の適合値は190ポンドです。実際の体重が200ポンドの場合は、残差は10となります。
解釈
残差をプロットし、モデルが適切であり、回帰仮定が満たされているかどうかを確認できます。残差を調べることにより、データに対するモデルの適合度に関して有用な情報を得ることができます。一般的に、残差はランダムに分布し、明確なパターンや異常値がありません。Minitabが、データに異常な観測値が含まれていると判断した場合は、これらの観測値が特定された、異常な観測値の適合値と診断の表が出力されます。ラベルが付けられた異常な観測値は、提示された回帰式にしっかりと従っていません。ただし、いくつかの異常な観測値があることは予測されていることです。たとえば、大きな残差の基準に基づくと、観測値の約5%は大きな残差を持つとしてフラグが付けられることが予測されます。異常な値に関する詳細は、異常な観測値を参照してください。
標準化残差
標準化残差は、残差（ei）をその標準偏差の推定値で割ったものです。
解釈
標準化残差を使用すると、外れ値を検出しやすくなります。2より大きく、-2より小さい標準化残差は、通常は大きなものであると見なされます。異常な観測値の適合値と診断の表では、これらの観測値が「R」で示されます。ラベルが付けられた観測値は、提示された回帰式にしっかりと従っていません。ただし、いくつかの異常な観測値があることは予測されています。たとえば、大きな標準化残差の基準に基づくと、観測値の約5%は大きな標準化残差を持つとしてフラグが付けられることが予測されます。詳細は、異常な観測値を参照してください。
標準化残差が役に立つのは、生の残差が外れ値を識別するものとして許容されない場合があるためです。生の残差の分散は、それに関連付けられたx値によって異なることがあります。この残差の不一致では、生の残差の大きさを評価するのが難しくなります。残差を標準化することで、異なる分散が共通の尺度に変換され、この問題は解消されます。
