平均
平均の表には、1つ以上のカテゴリ変数に基づく、グループに含まれる観測値の適合平均が表示されます。適合平均では、最小二乗からバランス型計画の平均応答値が予測されます。
解釈
適合平均により1つの因子の異なる水準の平均応答が推定され、その一方でほかの因子の水準も平均化されます。
平均表を使い、データ内の因子水準間の統計的に有意な差を把握します。各グループの平均値は、各母平均の推定値です。項のグループ平均値間の統計的に有意な差を探します。
主効果として、表は各因子内のグループとその平均値が表示されます。交互作用効果としては、可能性のある全てのグループの組み合わせが表示されます。交互作用項が統計的に有意な場合は、主効果の解釈では必ず交互作用効果も考慮してください。
これらの結果では、平均表は平均ユーザビリティと品質の評価が、方法、工場、方法*工場の交互作用でそれぞれどのように変わるかを示しています。方法と交互作用項は水準0.10のときに統計的に有意です。表は、方法1と方法2はそれぞれ平均ユーザビリティ評価の4.819と6.212に関連付けられていることを示しています。これらの平均間の差は、それに対応する品質評価の平均よりも大きくなっています。これにより、固有分析の解釈が裏付けられました。
しかし、方法*工場の交互作用項も統計的に有意なため、交互作用効果を考慮することなしに主効果を解釈しないでください。たとえば、交互作用項の表では、方法が1の場合、工場Cが最も高いユーザビリティ評価と最も低い品質評価に関連付けられてることを示しています。一方で、方法が2の場合は工場Aが最も高いユーザビリティ評価と最も高い品質評価の値と同等に近い評価に関連付けられています。
応答の最小二乗平均
| 有用性評価 | 品質評価 | |||
|---|---|---|---|---|
| 平均 | 平均の標準誤差 | 平均 | 平均の標準誤差 | |
| 方法 | ||||
| 方法1 | 4.819 | 0.165 | 5.242 | 0.193 |
| 方法2 | 6.212 | 0.179 | 6.026 | 0.211 |
| 工場 | ||||
| 工場A | 5.708 | 0.192 | 5.833 | 0.226 |
| 工場B | 5.493 | 0.232 | 5.914 | 0.273 |
| 工場C | 5.345 | 0.206 | 5.155 | 0.242 |
| 方法*工場 | ||||
| 方法1 工場A | 4.667 | 0.272 | 5.417 | 0.319 |
| 方法1 工場B | 4.700 | 0.298 | 5.400 | 0.350 |
| 方法1 工場C | 5.091 | 0.284 | 4.909 | 0.334 |
| 方法2 工場A | 6.750 | 0.272 | 6.250 | 0.319 |
| 方法2 工場B | 6.286 | 0.356 | 6.429 | 0.418 |
| 方法2 工場C | 5.600 | 0.298 | 5.400 | 0.350 |
平均の標準誤差
平均の標準誤差(平均のSE)では、同じ母集団から繰り返しサンプルを抽出した場合に得られる適合平均間の変動性が推定されます。
たとえば、ランダムサンプルである312個の配達時間に基づいた平均配達時間は3.80日、標準偏差は1.43日であるとします。この数値から求められる平均の標準誤差は、0.08日(1.43を312の平方根で割ったもの)です。同じ母集団から同じサイズのランダムサンプルを複数抽出すると、異なるサンプル平均の標準偏差はおよそ0.08日になります。
解釈
平均の標準誤差から、適合平均によって推定される母平均の正確さを判定します。
平均の標準誤差の値が小さいほど、母平均の推定値の精度が高いことを示します。通常、標準偏差が大きいと、平均の標準誤差が大きくなり、母平均の推定値の精度が低くなります。サンプルサイズは大きいほど平均の標準誤差が小さくなり、母平均の推定値の精度は高くなります。
平均(共変量)
共変量の平均値は、データの平均であり、すべての観測値の和を観測値の数で割って求められます。平均とは、すべてのサンプル値を1つの値で要約したもので、データの中心を表します。
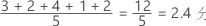
解釈
データの中心を表す1つの値で共変量を表すのに、平均を使います。
標準偏差
標準偏差とは、散布度、つまり平均からのデータの広がり方を表す最も一般的な測度です。多くの場合、母集団の標準偏差を表すには記号σ(シグマ)が使用されます。サンプルの標準偏差を表すには記号sが使用されます。
解釈
- およそ68%の値が1つの平均標準偏差に属します。
- 95%の値が2つの標準偏差に属します。
- 99.7%の値が3つの標準偏差に属します。
グループのサンプル標準偏差は、そのグループにおける母集団の標準偏差の推定値です。標準偏差は、信頼区間とp値を計算するために使用します。サンプル標準偏差が大きいほど、信頼区間は低く(広く)なり、検出力も低くなります。
分散分析では、すべての水準の母集団標準偏差が同じであると仮定されます。等分散を仮定できない場合、Minitab統計ソフトウェアで利用可能な一元配置分散分析(ANOVA)のオプション、ウェルチ検定の分散分析を使用します。
