Minitab® サポート

一般線形モデルの適合の変量因子と混合モデルの方法と計算式

Minitab についての 詳細
目的の方法または計算式を選択してください。

このトピックの内容

分散成分

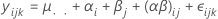
Minitabでは、変量因子に対してのみ分散成分が計算されます。2つの変量因子を持つモデルを用いた計算式を示します。

上の式で、αi、βj、(αβ)ij、εijkはすべて独立した確率変数です。変数は、平均0とこれらの計算式により与えられる分散により正規に分布されています。

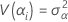
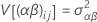
これらの分散は、分散成分です。この場合、分散成分が0に等しいという仮説を検定します。

固定因子Aおよび変量因子Bを持つ無制約型混合モデルは以下の計算式で表されます。

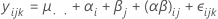
上の式で、αiは固定効果で、βj、(αβ)ij、εijkは平均を持たず、以下の分散を持つ無相関の確率変数です。

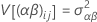
これらの分散は、分散成分です。Σα i = 0となります。

この情報はバランス型モデルに適用します。アンバランス型モデルやさらに複雑なモデルに関する情報は、Motgomery1およびNeter2を参照してください。

  1. D.C. Montgomery（1991年）Design and Analysis of Experiments第3版、John Wiley & Sons.
  2. J. Neter、W. Wasserman、M.H. Kutner（1985年）Applied Linear Statistical Models第2版、Irwin, Inc.

平均平方の期待値

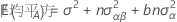
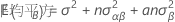
2つの因子A、Bを持つ変量効果モデルの平均平方の期待値を表す計算式は、以下になります。

固定因子Aおよび変量因子Bを持つ無制約型混合モデルの平均平方の期待値を表す計算式は以下になります。

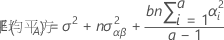
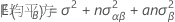
平均平方の期待値の計算に関するルール、およびアンバランス型モデルやさらに複雑なモデルに関する情報は、「モンゴメリー1」および「ニーター2」を参照してください。

  1. D.C. Montgomery (1991). Design and Analysis of Experiments, Third Edition. John Wiley & Sons.
  2. J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.

表記

用語説明
b因子Bの水準数
a因子Aの水準数
n因子水準の各組み合わせに含まれる観測値の数
σ2モデルの推定分散
Aの推定分散
Bの推定分散
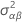ABの推定分散
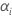Aの固定効果

変量因子を持つモデルのF統計量

分散分析の出力におけるF統計量の計算方法

各F統計量は平均平方の比です。分子は項の平均平方です。分母は分子の平均平方の期待値が分母の平均平方の期待値から対象となる効果だけ離れるように選択します。ランダム項の効果は、項の分散成分によって表されます。固定項の効果は、その項に関連付けられたモデル成分の平方和をその自由度で割ったものによって表されます。したがって、F統計量が高い場合、効果が有意であることを示します。

モデルのすべての項が固定の場合、各F統計量の分母は誤差の平均平方（MSE）です。ただし、ランダム項を含むモデルについては、MSEが常に正しい平均平方になるとは限りません。平均平方の期待値（EMS）を使用して何が分母に適しているかを判断できます。

例

固定因子「画面」と変量因子「技術」で分散分析を実行し、平均平方の予測値（EMS）について次の出力が得られたとします。
要因 各項に対する平均平方の期待値
(1)画面 (4) + 2.0000(3) + Q[1]
(2)技術 (4) + 2.0000(3) + 4.0000(2)
(3)画面*技術 (4) + 2.0000(3)
(4)誤差 (4)

括弧に入った数字は、要因番号の横に記載する項に関連付けられたランダム効果を示します。(2)は技術のランダム効果を表し、(3)は画面*技術の交互作用のランダム効果を表し、(4)は誤差のランダム効果を表します。誤差のEMSは誤差項の効果です。さらに、画面*技術のEMSは誤差項の効果に画面*技術の交互作用の効果の2倍を加えたものです。

画面*技術のF統計量を計算するには、画面*技術の平均平方を誤差の平均平方で割って、分子の期待値（画面*技術のEMS = (4) + 2.0000(3)）は分母の期待値（誤差のEMS = (4)）から交互作用の効果（2.0000(3)）だけ離れるようにします。したがって、F統計量が高い場合、画面*技術の交互作用が有意であることを示します。

Q[ ]が付いた数字は、要因番号の横に記載する項に関連付けられた固定効果を示します。たとえば、Q[1]は画面の固定効果です。画面のEMSは、誤差項の効果に画面*技術の交互作用の効果の2倍を加え、さらに画面の効果の定数倍を加えたものです。Q[1]は（b*n * sum((画面の水準の係数)**2)）を（a - 1）で割ったものです。aとbはそれぞれ画面と技術の水準の数で、nは反復数です。

画面のF統計量を計算するには、画面の平均平方を画面*技術の平均平方で割って、分子の期待値（画面のEMS = (4) + 2.0000(3) + Q[1]）が分母の期待値（画面*技術のEMS = (4) + 2.0000(3)）から画面に起因する期待値（Q[1]）だけ離れるようにします。したがって、F統計量が高い場合、画面の効果が有意であることを示します。

分散分析の出力で分散分析表のp値のそばに「x」とラベル「厳密なF検定ではありません」が表示される理由

項の正確なF検定とは、分子の平均平方の期待値が分母の平均平方の期待値から分散成分または対象の固定因子分だけ離れているものです。

ただし、こうした平均平方が計算できない場合もあります。この場合、Minitabでは近似のF検定の結果として得られる平均平方が使用され、p値のそばに「x」を表示して、F検定が正確でないことを示します。

たとえば、固定因子「補助材料」と変量因子「湖」で分散分析を実行し、平均平方の期待値（EMS）について次の出力が得られたとします。
要因 各項に対する平均平方の期待値
(1)補助材料 (4) + 1.7500(3) + Q[1]
(2)湖 (4) + 1.7143(3) + 5.1429(2)
(3)補助材料*湖 (4) + 1.7500(3)
(4)誤差 (4)

補助材料のF統計値は、補助材料の平均平方を補助材料*湖の交互作用の平均平方で割ったものです。補助材料の効果が非常に小さい場合、分子の期待値は分母の期待値と等しくなります。これは正確なF検定の例です。

ただし、湖の効果が非常に小さい場合、分子の期待値が分母の期待と等しくなるような平均平方は存在しない点に注意してください。したがって、Minitabでは近似のF検定が使用されます。この例では、湖の平均平方を補助材料*湖の交互作用の平均平方で割ります。これにより、湖の効果が非常に小さい場合、分子の期待値は分母の期待値とほぼ等しいという結果が得られます。

「F検定の分母がゼロまたは定義されていません」というメッセージについて

MinitabでF検定の分母がゼロまたは定義されていないというエラーが表示される理由は、次のいずれかです。
  • 少なくとも1つの誤差に対する自由度が存在しない場合があります。

  • 調整されたMS値が非常に小さく、F値やp値を表示する十分な精度に満たない場合。回避方法として、応答列を10倍にします。次に、同じ回帰モデルを実行しますが、応答にはこの新しい応答列を使用します。

    注

    応答値を10倍しても、Minitabで出力として表示されるF値およびp値には影響しません。ただし、それ以外の出力、具体的には逐次平方和、調整平方和、調整平均平方、適合値、適合値の標準誤差、残差列では小数点の位置が変わります。

分散分析の出力におけるF統計量の計算方法

各F統計量は平均平方の比です。分子は項の平均平方です。分母は分子の平均平方の期待値が分母の平均平方の期待値から対象となる効果だけ離れるように選択します。ランダム項の効果は、項の分散成分によって表されます。固定項の効果は、その項に関連付けられたモデル成分の平方和をその自由度で割ったものによって表されます。したがって、F統計量が高い場合、効果が有意であることを示します。

モデルのすべての項が固定の場合、各F統計量の分母は誤差の平均平方（MSE）です。ただし、ランダム項を含むモデルについては、MSEが常に正しい平均平方になるとは限りません。平均平方の期待値（EMS）を使用して何が分母に適しているかを判断できます。

例

固定因子「画面」と変量因子「技術」で分散分析を実行し、平均平方の予測値（EMS）について次の出力が得られたとします。
要因 各項に対する平均平方の期待値
(1)画面 (4) + 2.0000(3) + Q[1]
(2)技術 (4) + 2.0000(3) + 4.0000(2)
(3)画面*技術 (4) + 2.0000(3)
(4)誤差 (4)

括弧に入った数字は、要因番号の横に記載する項に関連付けられたランダム効果を示します。(2)は技術のランダム効果を表し、(3)は画面*技術の交互作用のランダム効果を表し、(4)は誤差のランダム効果を表します。誤差のEMSは誤差項の効果です。さらに、画面*技術のEMSは誤差項の効果に画面*技術の交互作用の効果の2倍を加えたものです。

画面*技術のF統計量を計算するには、画面*技術の平均平方を誤差の平均平方で割って、分子の期待値（画面*技術のEMS = (4) + 2.0000(3)）は分母の期待値（誤差のEMS = (4)）から交互作用の効果（2.0000(3)）だけ離れるようにします。したがって、F統計量が高い場合、画面*技術の交互作用が有意であることを示します。

Q[ ]が付いた数字は、要因番号の横に記載する項に関連付けられた固定効果を示します。たとえば、Q[1]は画面の固定効果です。画面のEMSは、誤差項の効果に画面*技術の交互作用の効果の2倍を加え、さらに画面の効果の定数倍を加えたものです。Q[1]は（b*n * sum((画面の水準の係数)**2)）を（a - 1）で割ったものです。aとbはそれぞれ画面と技術の水準の数で、nは反復数です。

画面のF統計量を計算するには、画面の平均平方を画面*技術の平均平方で割って、分子の期待値（画面のEMS = (4) + 2.0000(3) + Q[1]）が分母の期待値（画面*技術のEMS = (4) + 2.0000(3)）から画面に起因する期待値（Q[1]）だけ離れるようにします。したがって、F統計量が高い場合、画面の効果が有意であることを示します。

分散分析の出力で分散分析表のp値のそばに「x」とラベル「厳密なF検定ではありません」が表示される理由

項の正確なF検定とは、分子の平均平方の期待値が分母の平均平方の期待値から分散成分または対象の固定因子分だけ離れているものです。

ただし、こうした平均平方が計算できない場合もあります。この場合、Minitabでは近似のF検定の結果として得られる平均平方が使用され、p値のそばに「x」を表示して、F検定が正確でないことを示します。

たとえば、固定因子「補助材料」と変量因子「湖」で分散分析を実行し、平均平方の期待値（EMS）について次の出力が得られたとします。
要因 各項に対する平均平方の期待値
(1)補助材料 (4) + 1.7500(3) + Q[1]
(2)湖 (4) + 1.7143(3) + 5.1429(2)
(3)補助材料*湖 (4) + 1.7500(3)
(4)誤差 (4)

補助材料のF統計値は、補助材料の平均平方を補助材料*湖の交互作用の平均平方で割ったものです。補助材料の効果が非常に小さい場合、分子の期待値は分母の期待値と等しくなります。これは正確なF検定の例です。

ただし、湖の効果が非常に小さい場合、分子の期待値が分母の期待と等しくなるような平均平方は存在しない点に注意してください。したがって、Minitabでは近似のF検定が使用されます。この例では、湖の平均平方を補助材料*湖の交互作用の平均平方で割ります。これにより、湖の効果が非常に小さい場合、分子の期待値は分母の期待値とほぼ等しいという結果が得られます。

「F検定の分母がゼロまたは定義されていません」というメッセージについて

MinitabでF検定の分母がゼロまたは定義されていないというエラーが表示される理由は、次のいずれかです。
  • 少なくとも1つの誤差に対する自由度が存在しない場合があります。

  • 調整されたMS値が非常に小さく、F値やp値を表示する十分な精度に満たない場合。回避方法として、応答列を10倍にします。次に、同じ回帰モデルを実行しますが、応答にはこの新しい応答列を使用します。

    注

    応答値を10倍しても、Minitabで出力として表示されるF値およびp値には影響しません。ただし、それ以外の出力、具体的には逐次平方和、調整平方和、調整平均平方、適合値、適合値の標準誤差、残差列では小数点の位置が変わります。

Copyright © 2024 Minitab, LLC. All rights Reserved.