ステップ1:応答と項の関連が統計的に有意かどうかを判断する
- p値 ≤ α:関連性は統計的に有意です
- p値が有意水準以下の場合は、応答変数と項の間に統計的に有意な関連性が存在すると結論付けることができます。
- p値 > α:その関連性は統計的に有意ではありません
- p値が有意水準より大きい場合は、応答変数と項の間に統計的に有意な関連性があると結論付けることはできません。項を持たないモデルを再適合したいと考えるかもしれません。
- 固定因子が有意な場合は、すべての水準平均が等しいとは限らないと結論付けることができます。
- 変量因子が有意な場合は、その因子が応答の変動量に寄与していると結論できます。
- 交互作用項が有意な場合は、因子と応答の間の関係はその項の他の因子に依存します。こうしたケースでは、交互作用の影響を考慮せずに主要な影響を解釈すべきではありません。
平均表を使い、データ内の因子水準間の統計的に有意な差を把握します。各グループの平均値は、各母平均の推定値です。項のグループ平均値間の統計的に有意な差を探します。
主効果として、表は各因子内のグループとその平均値が表示されます。交互作用効果としては、可能性のある全てのグループの組み合わせが表示されます。交互作用項が統計的に有意な場合は、主効果の解釈では必ず交互作用効果も考慮してください。
因子情報
| 因子 | タイプ | 水準 | 値 |
|---|---|---|---|
| 時間帯 | 固定 | 2 | 1, 2 |
| 測定者 | ランダム | 3 | 1, 2, 3 |
| 設定 | 固定 | 3 | 35, 44, 52 |
厚さの分散分析
| 要因 | 自由度 | 平方和 | 平均平方 | F値 | p値 | |
|---|---|---|---|---|---|---|
| 時間帯 | 1 | 9.0 | 9.00 | 0.29 | 0.644 | |
| 測定者 | 2 | 1120.9 | 560.44 | 4.28 | 0.081 | x |
| 設定 | 2 | 15676.4 | 7838.19 | 73.18 | 0.001 | |
| 時間帯*測定者 | 2 | 62.0 | 31.00 | 4.34 | 0.026 | |
| 時間帯*設定 | 2 | 114.5 | 57.25 | 8.02 | 0.002 | |
| 測定者*設定 | 4 | 428.4 | 107.11 | 15.01 | 0.000 | |
| 誤差 | 22 | 157.0 | 7.14 | |||
| 合計 | 35 | 17568.2 |
モデル要約
| S | R二乗 | R二乗 (調整済み) |
|---|---|---|
| 2.67140 | 99.11% | 98.58% |
検定の誤差項
| 要因 | 分散成分 | 誤差項 | 各項に対する平均平方の期待値 (無制約型モデルを使用) | |
|---|---|---|---|---|
| 1 | 時間帯 | 4 | (7) + 6 (4) + Q[1, 5] | |
| 2 | 測定者 | 35.789 | * | (7) + 4 (6) + 6 (4) + 12 (2) |
| 3 | 設定 | 6 | (7) + 4 (6) + Q[3, 5] | |
| 4 | 時間帯*測定者 | 3.977 | 7 | (7) + 6 (4) |
| 5 | 時間帯*設定 | 7 | (7) + Q[5] | |
| 6 | 測定者*設定 | 24.994 | 7 | (7) + 4 (6) |
| 7 | 誤差 | 7.136 | (7) |
合成された検定の誤差項
| 要因 | 誤差DF | 誤差MS | エラーMSの合成 | |
|---|---|---|---|---|
| 2 | 測定者 | 5.12 | 130.9747 | (4) + (6) - (7) |
平均
| 時間帯 | N | 厚さ |
|---|---|---|
| 1 | 18 | 67.7222 |
| 2 | 18 | 68.7222 |
| 設定 | N | 厚さ |
|---|---|---|
| 35 | 12 | 40.5833 |
| 44 | 12 | 73.0833 |
| 52 | 12 | 91.0000 |
| 時間帯*設定 | N | 厚さ |
|---|---|---|
| 1 35 | 6 | 40.6667 |
| 1 44 | 6 | 70.1667 |
| 1 52 | 6 | 92.3333 |
| 2 35 | 6 | 40.5000 |
| 2 44 | 6 | 76.0000 |
| 2 52 | 6 | 89.6667 |
主要な結果:p値、平均表
設定は固定因子でこの主効果は有意です。この結果はコーティングの平均の厚さはすべての機械設定で同じではないことを示しています。
時間帯*設定は2つの固定因子と関わる交互作用効果です。この交互作用項は有意で、各因子と応答の関係は他の因子の水準に依存することを示しています。この場合、交互作用効果を考慮することなしに主効果を解釈しないでください。
これらの結果では、平均表は厚さの平均値が時間帯、装置の設定、および時間と装置設定の組み合わせにより変わることを示しています。設定は統計的に有意で、平均は装置設定間で異なります。しかし、時間帯*設定の交互作用項も統計的に有意なため、交互作用効果を考慮することなしに主効果を解釈しないでください。たとえば、交互作用項の表では、設定が44の場合、時間帯2がコーティングの厚みの増加に関連付けられてることを示しています。一方、設定が52の場合は時間帯1が厚みの増加に関連付けられています。
作業者は変量因子で、変量因子を含むすべての交互作用はランダムであるとみなされます。変量因子が有意な場合は、その因子が応答の変動量に寄与していると結論できます。作業者は水準0.05においては有意ではありませんが、作業者を含む交互作用効果は有意です。これらの交互作用効果は、作業者に起因する応答の変動量は、時間帯と機械の設定の両方に依存することを示しています。
ステップ2: データに対するモデルの適合度を判断する
データに対するモデルの適合度を判断するために、モデル要約表の適合度統計量を調査します。
- S
-
Sを使い、モデルがどの程度良好に応答を表示するか判断します。R2統計量のかわりにSを使い、定数を持たないモデルの適合を比較します。
Sは応答変数の単位で測定され、データ値と適合値の間の距離を表します。Sの値が小さければ小さいほど、モデルによる応答の記述が良好になります。ただし、Sの値が小さいだけでは、そのモデルが仮定を満たしているとは言い切れません。残差プロットを確認して仮定を検証する必要があります。
- R二乗
-
R2値が大きくなるほど、モデルのデータへの適合度は上がります。R2は常に0~100%の間の値になります。
R2はモデルに新しい予測変数を追加すると必ず大きくなります。たとえば、最適な5予測変数モデルのR2は必ず、最適な4予測変数モデルと少なくとも同じ大きさになります。したがって、R2値は同じ大きさのモデルの比較に最も便利です。
- R二乗(調整済み)
-
異なる数の予測変数を持つモデルを比較する場合は、調整済みR2を使用します。R2はモデルに予測変数を追加すると、それがモデルを改善しないとしても必ず大きくなります。調整済みR2値にはモデルに含まれる予測変数の数が組み入れられるため、正しいモデルの選択に役立ちます。
-
サンプルサイズが小さい場合、応答と予測との間の関係の強さが正確に推定されません。たとえば、より正確なR2が必要な場合、サンプルサイズを大きくする必要があります(40以上が一般的です)。
-
適合度統計量は、データに対するモデルの適合度を測る1つの測度に過ぎません。モデルに望ましい値がある場合でも、残差プロットを確認してモデルが仮定を満たしているかを検証する必要があります。
モデル要約
| S | R二乗 | R二乗 (調整済み) |
|---|---|---|
| 2.67140 | 99.11% | 98.58% |
主要な結果:S、R二乗、R二乗(調整済み)
この結果では、モデルはコーティングの厚さにおける99.11%の変動を説明しています。これらのデータで、R2値はモデルが良好にデータに適合していることを示しています。新しいモデルが別の予測変数と適合する場合は、調整済みR2値を使ってモデルの適合度を比較してください。
ステップ3:モデルが分析の仮説を満たすかどうか判断する
残差プロットを使用して、モデルが適切か、分析の仮定が満たされているかどうかを判断しやすくします。仮定を満たさない場合、そのモデルはデータにあまり適合しない可能性があり、結果の解釈は慎重に行う必要があります。
残差プロットのパターンを処理する方法の詳細は一般線形モデルの適合の残差プロットを参照し、ページ上部にある一覧の中から残差プロット名をクリックしてください。
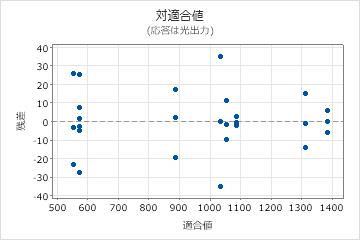
残差対適合値プロット
残差対適合値プロットを使用して、残差はランダムに分布し、均一な分散が存在するという仮定を検証します。点に特徴的なパターンがなく、0の両側にランダムにくるのが理想的です。
| パターン | パターンが示す意味 |
|---|---|
| 残差が適合値周辺に扇状または不均等に分散している | 不均一分散 |
| 曲線 | 高次の項の欠損 |
| ゼロから遠い点 | 外れ値 |
| ある点が他の点からX軸方向に遠く離れている | 影響力のある点 |
残差対順序プロット
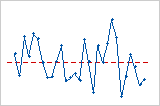
トレンド
シフト
周期
この残差対順序プロットでは、残差は中心線の周りにランダムに配置されているように見えます。残差が独立していないという証拠は存在しません。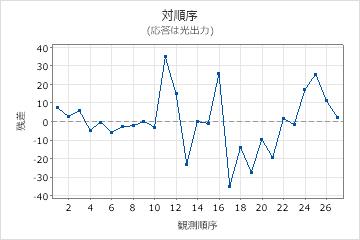
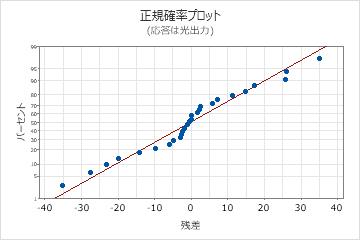
正規確率プロット
残差の正規確率プロットを使用して、残差が正規分布に従うという仮定を検証します。残差の正規確率プロットは、ほぼ直線になります。
| パターン | パターンが示す意味 |
|---|---|
| 直線ではない | 非正規性 |
| 直線から離れた点 | 外れ値 |
| 変化する傾き | 未確認の変数 |