方法
2因子のモデルでは、平均の分散は交互作用効果が有意か、主効果が全体平均と異なるかどうかを判断する手順です。二元平均分析では、データはバランス型でなければなりません。
平均
計算式
与えられた水準での因子に対する観測値の平均です。各因子水準の平均がグラフにプロットされます。
| i番目の水準での因子Aの平均 |
 |
| j番目の水準での因子Bの平均 |
 |
表記
| 用語 | 説明 |
|---|---|
| yi. | 因子Aのi番目水準の全観測値の合計 |
| y.j. | 因子Bのj番目水準の全観測値の合計 |
| a | Aの水準数 |
| b | Bの水準数 |
| n | 因子Aのi番目の水準および、因子Bのj番目の水準でのケースの数 |
全体平均(中心線)
計算式
サンプルに含まれる全ての観測値の平均です。Minitabでは主効果のグラフの中心線に全体平均を設定します。

表記
| 用語 | 説明 |
|---|---|
| y... | サンプルに含まれるすべての観測値の和 |
| a | Aの水準数 |
| b | Bの水準数 |
| n | 因子Aのi番目の水準および、因子Bのj番目の水準でのケースの数 |
主効果の決定線の上限と下限
決定限界は、因子水準平均が全体平均と異なっているかを示します。上側決定限界(UDL)または下側決定限界(LDL)の外側にある点は、全体平均とは有意に異なっています。
上側決定限界と下側決定限界の計算方法は、因子に含まれる水準の数と、各水準での観測値の数によって変わります。下に示す計算式は、因子Aの上側決定限界と下側決定限界を算出しています。因子Bの決定限界を計算するには、因子Aの項を因子Bの対応する項に置き換えます。
2水準因子
因子Aの上側決定限界と下側決定限界は次の計算式で算出されます。
- UDLA =
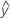 ...+ (.5) * hα* Sqrt[(MSE) * (2 / n1)]
...+ (.5) * hα* Sqrt[(MSE) * (2 / n1)] - LDLA =
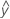 ...- (.5) * hα* Sqrt[(MSE) * (2 / n1)]
...- (.5) * hα* Sqrt[(MSE) * (2 / n1)]
ここで、ha = 絶対値(t(a / 2; abn - ab)、MSE = 誤差の平均平方(項A、B、ABの分散分析による)、およびn1= 因子Aの各水準における観測値数です。
3つ以上の水準を持つ因子
- UDLA =
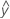 ...+ hα* Sqrt[MSE * (a - 1) / (a * n1)]
...+ hα* Sqrt[MSE * (a - 1) / (a * n1)] - LDLA =
 ...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
ここで、MSE = 誤差の平均平方(項A、B、ABの分散分析による)、a = 因子Aに含まれる因子水準数、およびn1= 因子の各水準での観測値数です。棄却値hαは、アルファ、プロットされる平均の数、および平均平方誤差の自由度によって異なります。hαの値は、「Nelson1の付録B」の表B.1を参照してください。
0.001と0.1の範囲を外れるα値の決定限界は次の計算式で算出されます。
- UDLA =
 ...+ hα* Sqrt[MSE * (a - 1) / (a * n1)]
...+ hα* Sqrt[MSE * (a - 1) / (a * n1)] - LDLA =
 ...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
ここで、MSE = 平均平方誤差(項A、B、ABの分散分析による)、n1 = 因子の各水準の観測値数、およびhα = 絶対値(t(α2, df))で、絶対値は、a2 = (1- (1- a )** (1 / a)) / 2、df = nT - ab(nT = サンプルに含まれる観測値の合計数)です。
- L.S.Nelson (1983)."Exact Critical Values for Use with the Analysis of Means", Journal of Quality Technology, 15, 40-44.
交互作用効果の決定線の上限と下限
決定限界は、交互作用が有意かどうかを示します。上側決定限界(UDL)または下側決定限界(LDL)の外側にある点は、その交互作用が統計的に有意であることを意味します。
因子A、Bの交互作用における上側決定限界と下側決定限界の一般的な計算式を以下に示します。項は、各因子に含まれる水準の数と観測値の数に基づいて別に定義されています。
- UDLAB = hα* Sqrt[MSE * (q / (a * b * n)]
- LDLAB = –hα* Sqrt[MSE * (q / (a * b * n)]
ここで、ha = 絶対値(t(α2, dfe))、a = 因子Aの水準数、b = 因子Bの水準数、n = 因子間の各交互作用に対する観測値数、q = 交互作用効果の自由度(a - 1)(b - 1)、dfe = 誤差に対する自由度abn - ab になります。
因子A、Bはともに2つの水準を持つ
- α2 = a / 2
因子Aは2つの水準、因子Bは3つ以上の水準を持つ
- α2 = (1- (1- a )** (1 / b)) / 2
上の式で、a = 因子Aの水準数、b = 因子Bの水準数になります。
因子Aは3つ以上の水準、因子Bは2つの水準を持つ
- α2 = (1- (1- a )** (1 / a)) / 2
上の式で、a = 因子Aの水準数、b = 因子Bの水準数になります。
因子A、Bはともに3つ以上の水準を持つ
- α2 = (1- (1- a )** (1 /a * b)) / 2
上の式で、a = 因子Aの水準数、b = 因子Bの水準数になります。
