方法
平均の分析は、個別の因子水準平均が全体平均(因子に含まれる全観測値の平均)と異なるかどうかを判断する手順です。下に示すのは、Minitabで一元配置のモデルの平均分析(ANOM)結果が計算される手順です。
- 各因子水準y̅i. (i = 1,…, r)での平均を計算します。
- すべての観測値y…の全体平均を計算します。
- 観測値の標準偏差の推定値spを計算します。
- 検定に選択された有意水準に対応する値で、決定線の上限と下限に使用される値のhαを決定します。
- 決定線の上限と下限を計算します(UDLとLDL)。
- 全体平均を中心線とし、各因子水準の平均を上方と下方の参照ラインでプロットします。
平均
計算式
各因子水準での観測値の平均です。各因子水準の平均がグラフにプロットされます。

表記
| 用語 | 説明 |
|---|---|
| ni | 因子水準iにおける観測値数 |
| yij | 因子水準i番目でのj番目の観測値 |
全体平均(中心線)
計算式
因子水準全体におけるすべての観測値の平均です。Minitabではグラフの中心線に全体平均を設定します。

表記
| 用語 | 説明 |
|---|---|
| y... | サンプルに含まれるすべての観測値の和 |
| nT | 合計観測数 |
標準偏差
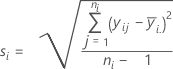
表記
| 用語 | 説明 |
|---|---|
| yij | 因子水準i番目での観測値 |
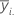 | 因子水準i番目での観測値の平均 |
| ni | i番目の因子水準の観測値数 |
併合標準偏差
すべての因子水準における推定変動です。併合標準偏差は、決定限界を計算するために使用します。
計算式
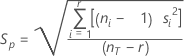
表記
| 用語 | 説明 |
|---|---|
| r | 水準数 |
| nT | 合計観測数 |
決定線の上限と下限
決定限界は、因子水準平均が全体平均と異なっているかを示します。上側決定限界(UDL)または下側決定限界(LDL)の外側にある点は、全体平均とは有意に異なっています。
上側決定限界と下側決定限界の計算方法は、因子に含まれる水準の数と、各水準での観測値の数によって変わります。
各水準において同数の観測値を持つ2水準因子
- UDL = y.. + hα sp* Sqrt(1/ nT)
- LDL = y.. - hα sp* Sqrt(1/ nT)
上の式で、hα = 絶対値(t(a / 2, nT - 2))、sp = 併合標準偏差、およびnT = 合計観測数です。
各水準において同数の観測値を持つ2つ以上の水準の因子
- UDL = y.. + hα sp* Sqrt[(r-1) / (rn1)
- LDL = y.. - hα sp* Sqrt[(r-1) / (rn1)
上の式で、r = 因子に含まれる水準数、n1 = 各水準における観測値数です。
自由度は(n1- 1) * rです。
0.001と0.1の範囲を外れるα値の決定限界は次の計算式で算出されます。
- UDL = y.. + hα sp* Sqrt[(nT - n1) / (nT* n1)
- LDL = y.. - hα sp* Sqrt[(nT - n1) / (nT* n1)
上の式で、hα = 絶対値(t(α2, df)で、α2 = (1- (1- a )** (1 / r)) / 2、df = nT- rです。
0.001と0.1間のα値に対するhαの算出については、「ネルソン1」を参照してください。
各水準において観測値数が同数ではない、2つ以上の水準を持つ因子
- UDLi = y.. + hα sp* Sqrt[(nT - ni) / (nT* ni)
- LDLi = y.. - hα sp* Sqrt[(nT - ni) / (nT* ni)
- L.S. Nelson (1983). "Exact Critical Values for Use with the Analysis of Means", Journal of Quality Technology, 15, 40-44.
