Gap合算の割り当ての平均合算と分散合算の計算

調整平均の計算式は次のとおりです。

μ_adj,i = μ_i + q_iμ_Pool

ここで、

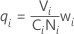
平均シフト係数が指定されていない場合は、平均合算 = 0となります。

調整標準偏差の計算式は次のとおりです。

σ²_adj,i = σ²_i + r_iσ²_Pool

ここで、

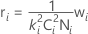
変動拡大係数が指定されておらず、Gapの規格限界がどちらも指定されていない場合は、分散合算 = 0となります。