多変量管理図とは
多変量管理図は、因子と応答の関係を表すグラフです。特にデータ分析の予備段階で分散分析データをグラフィック形式で表示し、データ、考えられる関係、および変動の根源的な原因を見るために使用します。多変量管理図は、交互作用を理解するのに特に便利です。
Minitabでは、最高4つの因子について多変量管理図が作成されます。管理図には、各因子の各水準における平均が表示されます。
2因子多変量管理図の例
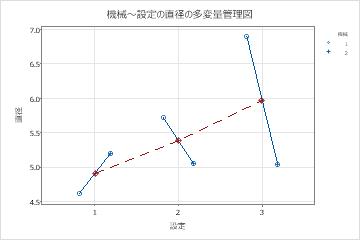
青い記号は、各機械のパイプ径平均を表します。赤の記号は、各設定のパイプの直径平均を表します。機械間の直径の変動は、他の設定よりも3を設定する場合にははるかに大きい。設定とマシンの間には相互作用があるようです。
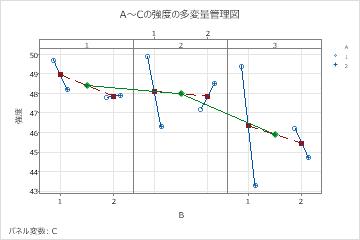
3因子多変量管理図の例
- 各パネルは因子Cの1水準を表します。緑色のダイヤモンドは、因子Cの各水準の平均を表します。緑色の線は、因子Cの水準の平均を結ぶ。
- 各パネルには、因子Bの各レベルに対応する2つのセクションがあります。赤い四角形は、因子Bの各水準の平均を表します。赤い破線は、因子Bの水準平均を結ぶ。
- 各セクションには、因子 A の各水準平均に対応する一連の記号があります。異なる記号は第3因子の各水準を表します。青実線は、因子Aの水準が意味する要素を接続します。
交互作用とは何か
応答を左右するある因子の効果が別の因子の水準に依存する場合、これら2つの因子は交互に作用します。因子AとBの間の交互作用は、ABと表記されます。
たとえば、帰宅する道順が2通りあるとします。その一方は高速道路を通るもので、他方は脇道を通るものです。どちらの道順も道のりはほぼ同じですが、制限速度は高速道路の方がはるかに高いので、 道路が空いている場合は、前者の方が後者より著しく短時間で帰宅できます。しかし、ラッシュアワーには高速道路が混雑するため、実際に脇道の方が短時間になります。
これは2つの因子、道順と1日の時間帯との間の交互作用の例で、この場合の応答は帰宅時間です。実際、これは交互作用の最も極端な例で、効果の方向が他因子の水準に依存して変化します。ラッシュアワーにも高速道路の方が早い場合、これも交互作用と考えられますが、この場合には高速道路の有利性がラッシュアワー時に減少すると捉えられます。
| ラッシュアワー以外 | ラッシュアワー | |
|---|---|---|
| 高速道路 | 30分 | 1時間 |
| 脇道 | 45分 | 45分 |
3元および4元の交互作用も分析できますが、これらの解釈はより複雑になります。
