ある品質エンジニアは、自社が製造する電球の寿命を評価したいと考えています。エンジニアは電球の標本を無作為に100個抽出し、燃え尽きるまでの点灯時間を記録します。エンジニアは許容限界の下限(電球の95%以上が点灯する時間)を計算しようとしています。
- 標本データを開く、 電球の寿命.MWX.
- を選択します。
- ドロップダウンリストから、1つ以上のサンプルが1つの列にあるを選択して、時間を入力します。
- オプションをクリックします。
- 許容限界区間から、下限を選択します。
- 各ダイアログボックスでOKをクリックします。
結果を解釈する
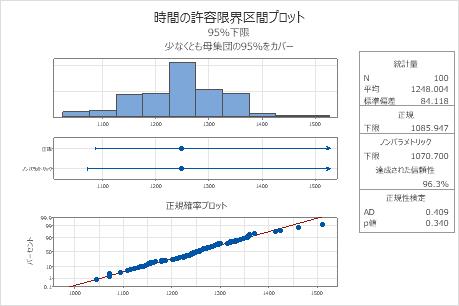
正規確率プロットは、プロットされた点がほぼ直線で、データが正規分布に従うということを表しています。さらに、正規性検定のp値は0.340で、これは有意水準(α = 0.05)よりも大きくなっています。従って、データが正規分布に従わないと判断する十分な証拠はありません。エンジニアは正規の方法による結果を使用できます。
正規下限は1085.947であるため、エンジニアは95%の信頼度で、電球の95%以上が約1086時間以上点灯すると、考えます。すべての電球では、平均点灯時間は約1248時間で、標準偏差は約84.1です。
方法
| 信頼水準 | 95% |
|---|---|
| 区間内の母集団のパーセント | 95% |
統計量
| 変数 | N | 平均 | 標準偏差 |
|---|---|---|---|
| 時間 | 100 | 1248.004 | 84.118 |
95%の下方許容限界
| 変数 | 正規法 | ノンパラメトリック法 | 達成された信頼性 |
|---|---|---|---|
| 時間 | 1085.947 | 1070.700 | 96.3% |