目的の方法または計算式を選択してください。
最尤推定値
分布におけるパラメータの最尤推定値は、パラメータに関する尤度関数の最大値を求めることによって計算されます。与えられたデータセットにおいて、最尤推定値は分布パラメータで最も可能性の高い値です。
ニュートン-ラフソンアルゴリズムは、分布パラメータの最尤推定値の計算に使用されます。ニュートン-ラフソンアルゴリズムは関数の最大値を求める反復数値方法です。1
注
Minitabでは、対数正規分布以外のすべての分布に対してパラメータ推定値が最尤法によって算出されます。対数正規分布に対しては、不偏推定値が計算されます。
確率分布
対数正規分布
| 確率密度関数 |
 |
| 累積分布関数 |
 |
| 平均 |
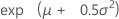 |
| 標準偏差 |
 |
| 用語 | 説明 |
|---|---|
| μ | 尺度パラメータ |
| σ | 形状パラメータ |
ガンマ分布
| 確率密度関数 |
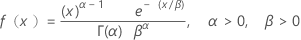 |
| 累積分布関数 |
 |
| 平均 | αβ |
| 標準偏差 | αβ2 |
| 用語 | 説明 |
|---|---|
| α | 形状パラメータ |
| β | 尺度パラメータ |
指数分布
| 確率密度関数 |
 |
| 累積分布関数 |
 |
| 平均 | θ |
| 標準偏差 | θ |
| 用語 | 説明 |
|---|---|
| θ | 尺度パラメータ |
最小極値分布
| 確率密度関数 |
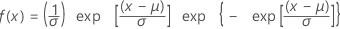 |
| 累積分布関数 |
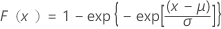 |
| 平均 |
 |
| 標準偏差 |
 |
| 用語 | 説明 |
|---|---|
| μ | 位置パラメータ |
| σ | 尺度パラメータ |
| Y | オイラーの定数(およそ0.5772) |
ワイブル分布
| 確率密度関数 |
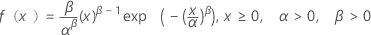 |
| 累積分布関数 |
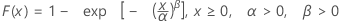 |
| 平均 |
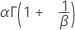 |
| 標準偏差 |
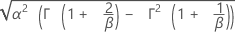 |
| 用語 | 説明 |
|---|---|
| α | 尺度パラメータ |
| β | 形状パラメータ |
最大極値分布
| 確率密度関数 |
 |
| 累積分布関数 |
 |
| 平均 |
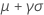 |
| 標準偏差 |
 |
| 用語 | 説明 |
|---|---|
| μ | 位置パラメータ |
| σ | 尺度パラメータ |
| Y | オイラーの定数(およそ0.5772) |
ロジスティック分布
| 確率密度関数 |
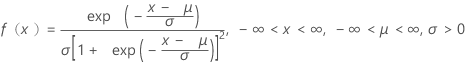 |
| 累積分布関数 |
 |
| 平均 | μ |
| 標準偏差 |
 |
| 用語 | 説明 |
|---|---|
| μ | 位置パラメータ |
| σ | 尺度パラメータ |
対数ロジスティック分布
| 確率密度関数 |
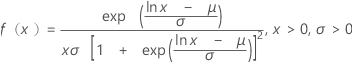 |
| 累積分布関数 |
 |
| 平均 |
 |
| 標準偏差 |
 |
| 用語 | 説明 |
|---|---|
| μ | 位置パラメータ |
| σ | 尺度パラメータ |
1 W. Murray, Ed. (1972). Numerical Methods for Unconstrained Optimization. Academic Press.
