対数正規分布
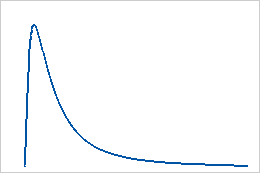
ランダム変数の対数が正規分布である場合に、対数正規分布を使用します。ランダム変数が0より大きい場合に使用します。たとえば、対数正規分布は、信頼性分析や金融分野(株価の動きのモデル化など)で使用されます。
対数正規分布は、位置パラメータと尺度パラメータによって定義される連続分布です。3パラメータ対数正規分布は、尺度、位置、およびしきい値パラメータで定義されます。
ガンマ分布
ガンマ分布を使用して、右方向に歪んだ0より大きい正のデータ値をモデル化します。ガンマ分布は、信頼性生存研究でよく使用されます。たとえば、電気部品の故障時期をガンマ分布で表すことができます。特定のタイプの電気部品のほとんどは同じ時期に故障しますが、故障するまでに長い時間がかかるものもあります。
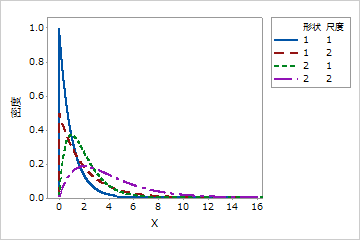
形状パラメータが整数の場合、ガンマ分布はアーラン分布と呼ばれることがあります。アーラン分布は、待ち行列理論の応用でよく使われています。
指数分布
指数分布を使用して、連続ポアソン工程における事象間の時間をモデル化します。独立した事象が一定の割合で発生すると仮定します。
この分布は、製品やシステム、待ち行列理論、およびマルコフ連鎖の信頼性分析などの幅広い用途に使用されます。
- 電子部品が故障するまでの時間
- ターミナルでの乗客の到着時間の間隔
- 顧客がサービスを受けるまで列に並んで待つ時間
- 債務不履行とみなされるまでの時間(信用リスクのモデリング)
- 放射性核が崩壊するまでの時間
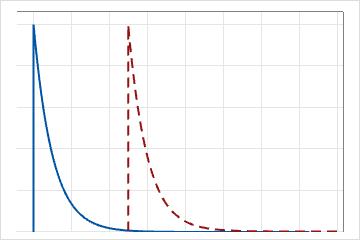
1パラメータ指数分布では、しきい値はゼロであり、分布は尺度パラメータによって定義されます。1パラメータ指数分布では、尺度パラメータは平均と等しいです。
無記憶性とは
指数分布の重要な特性はメモリレスであるということです。事象が発生する可能性は、過去の試験によって変わります。このため、発生率は一定のままです。
無記憶性とは、成分の残りの寿命が現在の年齢に左右されないことを意味します。たとえば、硬貨を投げるランダム試行回数は無記憶性を表します。損耗や破損のあるシステムは、今後使用中に障害を起こす可能性が高くなるため無記憶性ではありません。
最小極値分布と最大極値分布
最小極値分布
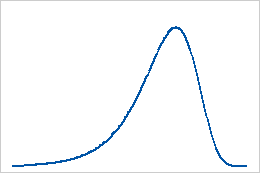
最大極値分布
ワイブル分布
ワイブル分布は、工学、医学的研究、品質管理、金融、および気象学などの幅広い用途のモデル化に使用できる、万能な分布です。たとえば、ワイブル分布は、故障までの時間データをモデル化するために信頼性分析に使用されることが多いです。また、工程能力分析の歪んだ工程データをモデル化するためにも使用されます。
ワイブル分布は、形状、尺度、しきい値パラメータによって説明され、3パラメータワイブル分布としても知られています。しきい値パラメータがゼロの場合は、2パラメータワイブル分布と呼ばれます。2パラメータワイブル分布は、正の変数のみで定義されます。3パラメータワイブル分布は、ゼロと負のデータとも連携できますが、2パラメータワイブル分布のすべてのデータはゼロよりも大きくなければなりません。
パラメータの値に応じて、ワイブル分布はさまざまな形状になります。
- 形状パラメータの影響
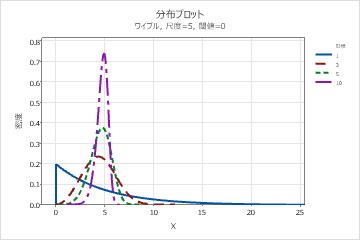
- 形状パラメータは、データがどのように分布するかを表します。3の形状は正規曲線に近似します。1などの低い値の形状は、右方向に歪んだ曲線になります。10などの高い値の形状は、左方向に歪んだ曲線になります。
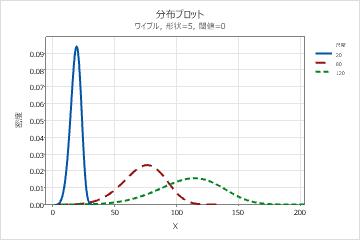
- 尺度パラメータの影響
- 尺度(特性寿命)はデータの63.2%の百分位です。尺度は、しきい値に対するワイブル曲線の位置を定義し、平均が正規曲線の位置を定義する方法と似ています。たとえば、尺度20は、装置の63.2%がしきい値時刻後20時間以内に故障することを示します。
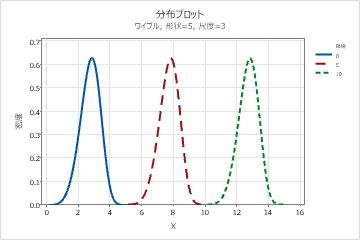
- しきい値パラメータの影響
- しきい値パラメータは、分布の0からのシフトを説明します。負のしきい値では分布が左側にシフトし、正のしきい値では分布が右側にシフトします。すべてのデータはしきい値よりも大きくなければなりません。2パラメータワイブル分布は、しきい値3パラメータワイブル分布と同じですが、しきい値は0になります。たとえば、3パラメータワイブル(3,100,50)の形状と分布は2パラメータワイブル(3,100)と同じですが、0の右側に50単位ほどシフトされています。
ロジスティック分布
ロジスティック分布を使用すると、正規分布よりも裾が長くて尖度が高いデータ分布をモデル化できます。
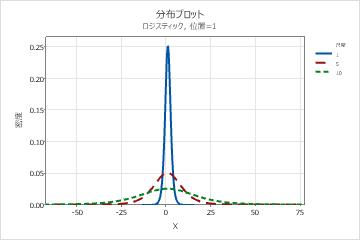
- 尺度パラメータの効果
- 次のグラフは、ロジスティック分布でのさまざまな尺度パラメータ値の影響を示しています。
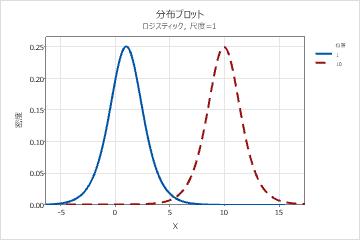
- 位置パラメータの効果
- 次のグラフは、ロジスティック分布でのさまざまな位置パラメータ値の影響を示しています。
対数ロジスティック分布
対数ロジスティック分布は、変数の対数がロジスティック分布に従う場合に使用します。たとえば、成長モデルで使用されたり、生物統計学や経済学などの分野で2値応答をモデル化するときに使用されます。
対数ロジスティック分布は、尺度パラメータと位置パラメータによって定義される連続分布です。3パラメータ対数ロジスティック分布は、尺度、位置、およびしきい値パラメータで定義されます。
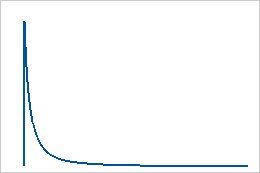
対数ロジスティック分布は、フィスク分布としても知られています。
