このトピックの内容
ランチャート
ランチャートには、工程データが収集順にプロットされます。 ランチャートを使用して、特別原因による変動の存在を示すデータのパターンまたはトレンドを探します。
解釈
データのパターンは、変動の原因が特別原因にあり、調査して修正する必要があることを示します。ただし、一般原因による変動は、工程に固有の、つまり工程の性質としての変動です。特別原因ではなく、一般原因のみが工程出力に影響している場合、工程は安定します。工程に存在するのが一般原因のみの場合、データはランダム性を示します。
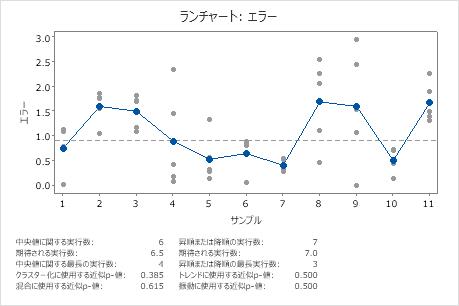
中央値付近の実行数
中央値付近の連数は、中央値より上の連の合計数と、中央値より下の連の合計数の和です。
中央値付近の連とは、中心線から見て同じ側にある1つ以上の連続する点のことです。連は、点をつなぐ線が中心線と交差するときに終わります。新しい連は、次にプロットされる点から始まります。
解釈
- 実行1には点1が含まれます。
- 実行2には点2と3が含まれます。
- 実行3には点4、5、6、および7が含まれます。
- 実行4には点8と9が含まれます。
- 実行5には点10が含まれます。
- 実行6には点11が含まれます。

中央値付近で期待される実行数
中央値付近で期待される実行数は、データがランダムに分布する場合に、データに含まれることが期待される実行の数です。
解釈
期待される実行数を実際の実行数と比較します。実行数が期待される数より多い場合は、データが2つの母集団から収集されたこと(混合)を示す可能性があります。実行数が期待される数より少ない場合は、データのクラスター化を示す可能性があります。p値を使用して統計的有意性を調べます。

中央値付近の最長の実行
中央値の上下の最長連の点の数。中心線上にプロットされる点は、中央値の下の連に属します。
解釈

クラスター化のp値を近似する
p値は帰無仮説を棄却するための証拠を測定する確率です。確率が低いほど帰無仮説を棄却するための強力な証拠となります。
p値を使用して、データがランダムに分布しているかどうかを判断します。帰無仮説は、データはランダムに分布しているというものです。
解釈
指定した有意水準より小さいp値は、クラスター化の傾向があることを示します。通常は、有意水準(αまたはアルファとも呼ばれる)として0.05が適切です。有意水準0.05は、データが実際にはランダムに分布しているのに、非ランダムパターンが存在すると結論付けるリスクが5%あることを示します。
- p値 ≤ α: 平均の差は有意に異なります(H0を棄却する)
- p値が有意水準以下の場合は、帰無仮説を棄却します。データはランダムに分布していないと結論付けることができます。
- p値 > α: 平均値の差は有意に異なりません(H0を棄却しない)
- p値が有意水準よりも大きい場合は、帰無仮説を棄却できません。データに非ランダムパターンがあると結論付けるだけの十分な証拠はありません。ただし、データはランダムに分布すると結論付けることもできません。

混合のp値を近似する
p値は帰無仮説を棄却するための証拠を測定する確率です。確率が低いほど帰無仮説を棄却するための強力な証拠となります。
p値を使用して、データがランダムに分布しているかどうかを判断します。帰無仮説は、データはランダムに分布しているというものです。
解釈
指定した有意水準未満のp値は、混合の傾向があることを示します。通常は、有意水準(αまたはアルファとも呼ばれる)として0.05が適切です。有意水準0.05は、データが実際にはランダムに分布しているのに、非ランダムパターンが存在すると結論付けるリスクが5%あることを示します。
- p値 ≤ α: 平均の差は有意に異なります(H0を棄却する)
- p値が有意水準以下の場合は、帰無仮説を棄却します。データはランダムに分布していないと結論付けることができます。
- p値 > α: 平均値の差は有意に異なりません(H0を棄却しない)
- p値が有意水準よりも大きい場合は、帰無仮説を棄却できません。データに非ランダムパターンがあると結論付けるだけの十分な証拠はありません。ただし、データはランダムに分布すると結論付けることもできません。

上昇または下降の実行数
上昇または下降の連の数は、データ内の上向きの連と下向きの連の合計数です。
上昇連は、増大する一方の連続する点による上向きの連です。下降連は、減少する一方の連続する点による下向きの連です。連は芳香(上昇または下降)が変わるときに終わります。たとえば、前の値がその次の値より小さい場合に上昇連が始まり、後続の値がその次の点の値より大きくなるまで続き、そこから下降連が始まります。
Minitabでは、値の等しい連続する観測値で構成されるフラット実行を下降実行の一部として数えます。
解釈
- 点2は実行1の終わりです。
- 点5は実行2の終わりです。
- 点6は実行3の終わりです。
- 点7は実行4の終わりです。
- 点8は実行5の終わりです。
- 点10は実行6の終わりです。
- 点11は実行7の終わりです。

フラット実行の解釈方法
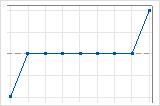
上昇および下降の3つの実行
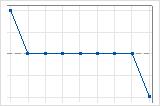
1つの下降実行
上昇または下降の期待される実行数
上昇または下降の期待される実行数は、データがランダムに分散する場合に、データに含まれることが予期される実行の数です。
解釈
期待される実行の数を実際の実行数と比較します。実行数が期待数より多い場合は、データに振動がある可能性があることを示します。実行数が期待数より少ない場合は、データにトレンドがある可能性があることを示します。

昇順または降順の最長実行数:
上昇または下降の最長連の点の数。
解釈

トレンドのp値を近似する
p値は帰無仮説を棄却するための証拠を測定する確率です。確率が低いほど帰無仮説を棄却するための強力な証拠となります。
p値を使用して、データがランダムに分布しているかどうかを判断します。帰無仮説は、データはランダムに分布しているというものです。
解釈
指定した有意水準未満のp値は、トレンドの傾向を示します。通常は、有意水準(αまたはアルファとも呼ばれる)として0.05が適切です。有意水準0.05は、データが実際にはランダムに分布しているのに、非ランダムパターンが存在すると結論付けるリスクが5%あることを示します。
- p値 ≤ α: 平均の差は有意に異なります(H0を棄却する)
- p値が有意水準以下の場合は、帰無仮説を棄却します。データはランダムに分布していないと結論付けることができます。
- p値 > α: 平均値の差は有意に異なりません(H0を棄却しない)
- p値が有意水準よりも大きい場合は、帰無仮説を棄却できません。データに非ランダムパターンがあると結論付けるだけの十分な証拠はありません。ただし、データはランダムに分布すると結論付けることもできません。

振動のp値を近似する
p値は帰無仮説を棄却するための証拠を測定する確率です。確率が低いほど帰無仮説を棄却するための強力な証拠となります。
p値を使用して、データがランダムに分布しているかどうかを判断します。帰無仮説は、データはランダムに分布しているというものです。
解釈
p値が指定した有意水準より小さい値の場合は、振動の傾向があること示しています。通常は、有意水準(αまたはアルファとも呼ばれる)として0.05が適切です。有意水準0.05は、データが実際にはランダムに分布しているのに、非ランダムパターンが存在すると結論付けるリスクが5%あることを示します。
- p値 ≤ α: 平均の差は有意に異なります(H0を棄却する)
- p値が有意水準以下の場合は、帰無仮説を棄却します。データはランダムに分布していないと結論付けることができます。
- p値 > α: 平均値の差は有意に異なりません(H0を棄却しない)
- p値が有意水準よりも大きい場合は、帰無仮説を棄却できません。データに非ランダムパターンがあると結論付けるだけの十分な証拠はありません。ただし、データはランダムに分布すると結論付けることもできません。

