元データと変換データの確率プロット
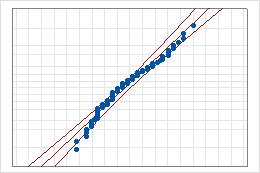
- 中央の線
- パラメータの最尤推定値に基づいて分布で期待される百分位数です。
- 信頼境界線
- 左側の曲線は、百分位数の信頼区間の下側の境界を示します。右側の曲線は、百分位数の信頼区間の上側の境界を示します。
解釈
正規確率プロットを使用して、元データと変換データの正規分布に対する適合度を評価します。
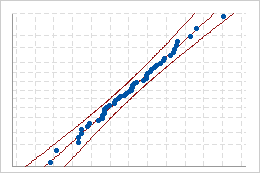
うまくあてはまる
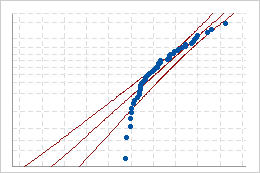
よくあてはまらない
注
元データが正規分布に従う場合、Minitabには、確率プロットが1つだけ表示され、Johnson変換は実行されません。
N
サンプル内の非欠損値の数。Nはすべての観測値の数です。
| 合計 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
解釈
Nは、サンプルサイズを評価するために使用します。
重要
非常に小さいか非常に大きいサンプルからの結果を解釈する場合は、注意を要します。サンプルサイズが非常に小さい場合は、適合度検定の検出力が分布からの有意な偏差を検出するのに十分ではない可能性があります。サンプルサイズが非常に大きい場合は、検定の検出力が非常に強く、現実的に有意ではない分布からの小さな偏差が検出される可能性があります。p値に加えて、確率プロットを使用して分布の適合を評価してください。
AD
Anderson-Darling適合度統計量(AD)は、(選択した分布に基づく)適合線と(データ点に基づく)ノンパラメトリックステップ関数の間の変動の測度です。Anderson-Darling統計量は、分布の裾のほうが重み付けが大きい二乗距離です。
解釈
Minitabでは、Anderson-Darling統計量を使用してp値を計算します。p値は、データが分布に従うという帰無仮説を棄却する証拠を測定する確率です。
一般に、Anderson-Darling統計量の値が大幅に小さくなっている場合は、データが分布により緊密に従うことを示しています。ただし、AD統計量は分布の種類が異なれば分布の仕方も異なるため、AD値どうしが近い値の場合は異なる分布間でAD値を直接比較することは避けてください。異なる分布の適合度をより良い方法で比較するには、確率プロット、p値、および工程に関する知識などの追加基準を使用してください。
p値
元データ値と変換データ値の場合、Minitabでは、Anderson-Darling(AD)正規性検定のp値が報告されます。p値は帰無仮説を棄却するための証拠を測定する確率です。AD正規性検定の場合、帰無仮説は、データは正規分布に従うというものです。したがって、p値が小さいほど、データが正規分布に従わないことの強力な証拠となります。
解釈
p値を使用して、元データと変換データが正規分布に従うかどうかを評価します。一般に、p値が大きいほど、データにうまくあてはまることを示します。
- p値がα値より小さい場合は、正規分布がうまくあてはまらないことを示します。
- p値がα値以上の場合は、分布の適合度が低いことを示す十分な証拠がないことを示します。その場合は、データは正規分布に従うと仮定することができます。
Johnson変換が有効な場合、変換データのp値はα値より大きくなります。
重要
非常に小さいか非常に大きいサンプルからの結果を解釈する場合は、注意を要します。サンプルサイズが非常に小さい場合は、適合度検定の検出力が分布からの有意な偏差を検出するのに十分ではない可能性があります。サンプルサイズが非常に大きい場合は、検定の検出力が非常に強く、現実的に有意ではない分布からの小さな偏差が検出される可能性があります。p値に加えて、確率プロットを使用して分布の適合を評価してください。
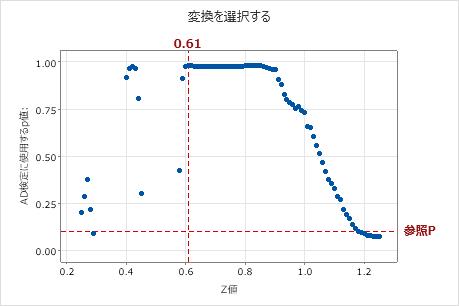
変換の選択グラフ
変換の選択グラフには、異なるJohnson変換関数でのZ値ごとに、AD正規性検定によって計算されたp値がプロットされます。広範な分布の場合、Johnson変換では、最適Zを見つけるために0.25から1.25の範囲で増分が0.01のZのグリッドを使用します。Minitabでは、Zごとに変換後データのp値を計算し、最大p値が分析で指定されたp値基準よりも大きくなっている変換関数を選択します。
解釈
変換の選択グラフを使用して、Johnson変換関数を選択してデータの最適適合を出力する方法を視覚化します。水平参照ラインには、分析で指定されたp値基準が表示されます。垂直参照ラインには、最適適合を出力する変換のZ値が表示されます。この最大Z値は、AD正規性検定の最小p値に相当します。
注
グラフの下の表(ここには示されていません)には、最適変換関数のパラメータ推定値が表示されます。Johnson変換関数の場合にMinitabで使用されるアルゴリズムの詳細については、個別の分布の識別での変換の方法と計算式に移動し、「Johnson変換の方法と計算式」をクリックします。
最適適合のp値
最適適合のp値は、正規分布に対する変換データの最適な適合が得られるJohnson変換関数のp値を示します。直近の小数点以下3桁の数に四捨五入されるp値は、変換データの確率プロットにも表示されます。
p値の解釈方法の詳細は、p値についてのセクションを参照してください。
最適適合が得られるJohnson変換関数をMinitabで選択する方法の詳細は、「変換グラフの選択」についてのセクションを参照してください。
最適適合のZ
最適適合のZ値は、正規分布に対する変換データの適合度が最大になるJohnson変換関数でのZ値を指します。最適Z値は、最適変換グラフに示されときの最適適合のp値に対応します。
MinitabでZ値を使用して最適適合のJohnson変換関数を選択する方法の詳細は、「変換グラフの選択」についてのセクションを参照してください。
最適変換タイプ
Johnson変換では、3種類の分布族(SB、SL、およびSU)のいずれか1つを最適な族として選択します(ここで、B、L、およびUは、限界あり、対数正規、および制限なしを意味します)。Mintiabでは、選択された分布関数を使用して、正規分布に従うようにデータを変換します。
Johnson変換関数を定義するためにMinitabで使用されるアルゴリズムの詳細は、個別の分布の識別での変換の方法と計算式に移動し、「Johnson変換の方法と計算式」をクリックします。
Johnson変換関数
Minitabには、最適適合を算出するJohnson変換関数のパラメータが表示されます。Minitabでは、この関数を使用して元データを変換します。
たとえば、Johnson変換関数が0.762475 + 0.870902 × Ln((X – 46.3174 ) / (59.6770 – X))であるとします。Xの元データの値が50の場合、50の変換データ値は、0.762475 + 0.870902 × Ln((50 – 46.3174) / (59.6770 – 50))として計算され、–0.07893となります。
注
すべての変換データの値をワークシートに保存するには、分析を実行するときの保存列を入力します。
Johnson変換関数を定義するためにMinitabで使用されるアルゴリズムの詳細は、個別の分布の識別での変換の方法と計算式に移動し、「Johnson変換の方法と計算式」をクリックします。
