このトピックの内容
Box-Cox変換
Box-Cox変換は、次の表に示すように、変換によって標準化された変数の標準偏差を最小化するλ値を推定します。結果として得られる変換は、λ ҂ 0の場合はYλで、λ = 0の場合はln Yです。
Box-Cox法では、さまざまな種類の変換が探索されます。次の表は、いくつかの一般的な変換を示しています。ここで、Y'はデータYの変換です。
| λ値 | 変換 |
|---|---|
 |
 |
 |
 |
 |
 |
 |
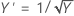 |
 |
 |
Johnson変換のアルゴリズム
Johnson変換では、3種類の分布族の中から最適な1つを選択して、正規分布に従うようにデータを変換します。
| Johnson族 | 変換関数 | 範囲 |
|---|---|---|
| SB | γ + η ln [(x – ε) / (λ + ε – x)] | η, λ > 0, –∞ < γ < ∞ , –∞ < ε < ∞, ε < x < ε + λ |
| SL | γ + η ln (x – ε) | η > 0, –∞ < γ < ∞, –∞ < ε < ∞, ε < x |
| SU | γ + η Sinh–1 [(x – ε) / λ] , where
Sinh–1(x) = ln [x + sqrt (1 + x2)] |
η, λ > 0, –∞ < γ < ∞, –∞ < ε < ∞, –∞ < x < ∞ |
このアルゴリズムでは、次のプロシージャを使用します。
- Johnson系の可能な限りすべての変換関数を考慮します。
- 『Chou, et al.』1で説明されている方法を使用して、関数内のパラメータを推定します。
- 変換関数を使用してデータを変換します。
- 変換されたデータのAnderson-Darling統計量とp値を計算します。
- 変換ダイアログボックスで指定するp値基準(デフォルトは0.10)より大きい最大p値を使用する変換関数を選択します。基準を超えるp値がない場合、変換は適切に行われません。
表記
| 用語 | 説明 |
|---|---|
| SB | 変数が限界あり(B)のJohnson族分布 |
| SL | 変数が対数正規(L)のJohnson族分布 |
| SU | 変数が限界なし(U)のJohnson族分布 |
Johnson変換についての詳細は、『Chou, et al.1』を参照してください。
確率プロット、百分位数、およびそれらの信頼区間についての詳細は、個別の分布の識別の分布の方法と計算式を参照してください。
1 Y. Chou, A.M. Polansky, and R.L. Mason (1998). "Transforming Nonnormal Data to Normality in Statistical Process Control", Journal of Quality Technology, 30, April, 133–141
