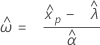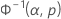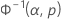確率プロット
確率プロットは次からなります。
- 点：大きさの順に並べたデータセットの確率に対応する推定百分位数です。
- 中央の線：パラメータの最尤推定値に基づく分布の期待される百分位数。分布がデータにうまくあてはまる場合、点は中央の線に沿って位置します。
推定確率
Minitabでは、次の方法を使用して、プロット点の計算に使用される確率（P）を推定します。
- 中央値順位（Benardの方法）
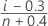
- 平均順位（Herd-Johnson推定）
- 修正されたKaplan-Meier（Hazen）
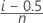
- Kaplan-Meier製品限界推定
表記
| 用語 | 説明 |
|---|---|
| n | 観測値数 |
| i | i番目の観測値x(i)の順位。x(1)、x(2)、... x(n)は順序統計量、または最小値から最大値の順に順序付けされたデータ |
プロット点
確率プロットの中央の線は、この表でのx座標とy座標の計算を使用して描画されます。
| 分布 | x座標 | y座標 |
|---|---|---|
| 最小極値 | x | ln(–ln(1 – p)) |
| 最大極値 | x | ln(–ln p) |
| ワイブル | ln(x) | ln(–ln(1 – p)) |
| 3-パラメータワイブル | ln(x – しきい値) | ln(–ln(1 – p)) |
| 指数 | ln(x) | ln(–ln(1 – p)) |
| 2-パラメータ指数 | ln(x – しきい値) | ln(–ln(1 – p)) |
| 正規 | x | Φ–1norm |
| 対数正規 | ln(x) | Φ–1norm |
| 3-パラメータ対数正規 | ln(x – しきい値) | Φ–1norm |
| ロジスティック | x |
 |
| 対数ロジスティック | ln(x) |
 |
| 3-パラメータ対数ロジスティック | ln(x – しきい値) |
 |
| ガンマ | x | Φ–1gamma |
| 3-パラメータガンマ | ln(x – しきい値) | Φ–1gamma |
注
プロット点は特定の分布には依存しないので、どの確率プロットを作成した場合も、変換前であればプロット点は同じです。ただし、適合線は選択するパラメトリック分布によって異なります。
表記
| 用語 | 説明 |
|---|---|
| p | 推定確率 |
| Φ-1norm | 標準正規分布の逆累積分布関数によって返されるpの値 |
| Φ-1gamma | 不完全ガンマ分布の逆累積分布関数によって返されるpの値 |
| ln(x) | xの自然対数 |
百分位数および百分位数の標準誤差
百分位数はスケールが100の値で、その値以下になる分布のパーセントを示します。Minitabには、デフォルトで、一般的な百分位数のパラメトリック分布分析の百分位数の表が表示されます。
百分位数の推定値の標準誤差は、変動の平方根です。
, 
, 
, 
, 
, 
, 
, 
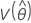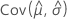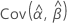、および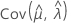 
は、Fisher情報行列の逆行列の適切な要素から取られた、μ、σ、α、β、λ、およびθのMLEの分散と共分散を意味します。
百分位数と分散の推定値を求めるために使用される計算式は次のとおりです。
最小極値分布
- 百分位数
-
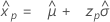
- 分散
-
最大極値分布
- 百分位数
-
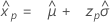
- 分散
-
ワイブル分布
- 百分位数
-
- 分散
-
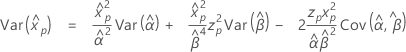
3-パラメータワイブル分布
- 百分位数
-
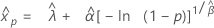
- 分散
-
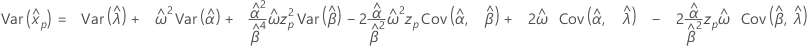
指数分布
- 百分位数
-
- 分散
-
2-パラメータ指数分布
- 百分位数
-
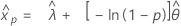
- 分散
-
正規分布
- 百分位数
-
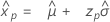
- 分散
-
対数正規分布
- 百分位数
-
- 分散
-
3-パラメータ対数正規分布
- 百分位数
-
- 分散
-
ロジスティック分布
- 百分位数
-
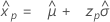
- 分散
-
対数ロジスティック分布
- 百分位数
-
- 分散
-
3-パラメータ対数ロジスティック分布
- 百分位数
-
- 分散
-
ガンマ分布
- 百分位数
-
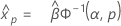
- 分散
-
-
ここで、
は、規則化された不完全ガンマ分布の逆分布
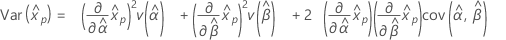
3-パラメータガンマ分布
- 百分位数
-
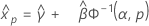
- 分散
-
-
ここで、
は、規則化された不完全ガンマ分布の逆分布
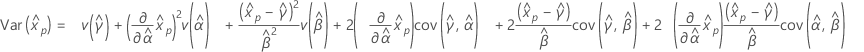
百分位数に対する信頼限界
| 分布 | 信頼限界 |
|---|---|
| 最小極値 |
 |
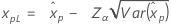| 最大極値 |
 |
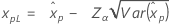| 正規 |
 |
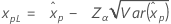| ロジスティック |
 |
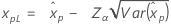| ワイブル |
 |
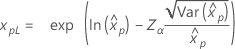| 指数 |
 |
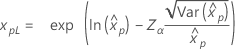| 対数正規 |
 |
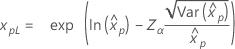| 対数ロジスティック |
 |
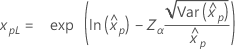| 3-パラメータワイブル |
If λ < 0:
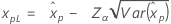 If λ ≥ 0:
  |
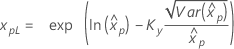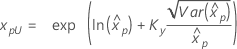| 2-パラメータ指数 |
If λ < 0:
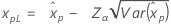 If λ ≥ 0:
  |
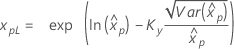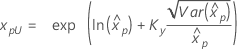| 3-パラメータ対数正規 |
If λ < 0:
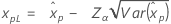 If λ ≥ 0:
  |
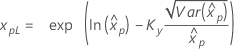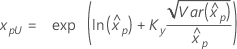| 3-パラメータ対数ロジスティック |
If λ < 0:
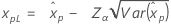 If λ ≥ 0:
  |
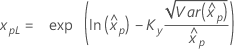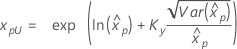表記
| 用語 | 説明 |
|---|---|
| Kγ | 標準正規分布の(1 + γ) / 2百分位数 |
