個別の分布の識別で使用されるすべての変換の定義と解釈について解説します。
このトピックの内容
Box-Cox変換(λ)
個別の分布の識別を実行するときにBox-Cox変換を含める場合、Minitabでは、変換で使用されるラムダ(λ)の値を報告します。
Box-Cox変換では、以下のようにしてλ値を推定し、標準化された変換変数の標準偏差を最小化します。出力される変換は、λ ≠ 0の場合にYλ、およびλ = 0の場合にIn Yです。
この方法では、多くのタイプの変換内を検索します。以下の表に、一般的な変換方法をいくつか示します(Y'はデータYの変換データ)。
| ラムダ(λ)値 | 変換 |
|---|---|
 |
 |
 |
 |
 |
 |
 |
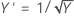 |
 |
 |
Johnson変換関数
個別の分布の識別を実行するときにJohnson変換を含めると、Minitabでは、データの変換に使用した関数を報告します。たとえば、Johnson変換関数が0.762475 + 0.870902 × Ln((X – 46.3174 ) / (59.6770 – X))であるとします。Xの元データの値が50の場合、50の変換データ値は、0.762475 + 0.870902 × Ln((50 – 46.3174) / (59.6770 – 50))として計算され、–0.07893となります。
Johnson変換関数を定義するためにMinitabで使用されるアルゴリズムの詳細は、個別の分布の識別での変換の方法と計算式を参照してください。
