確率プロット
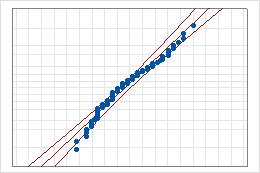
- 中央の線
- パラメータの最尤推定値に基づいて分布で期待される百分位数です。
- 信頼境界線
- 左側の曲線は、百分位数の信頼区間の下側の境界を示します。右側の曲線は、百分位数の信頼区間の上側の境界を示します。
解釈
確率プロットは、データが各分布に従う程度を評価するために使用します。
分布がデータにうまくあてはまる場合、点の位置は適合分布線の付近になります。直線からの逸脱は、その適合が許容されないことを示します。
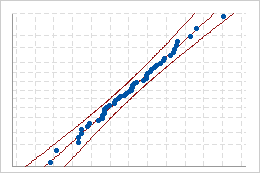
うまくあてはまる
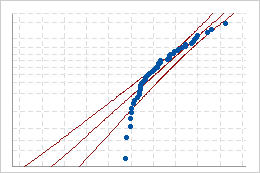
よくあてはまらない
確率プロットに加えて、AD p値などの適合度の測度および尤度比検定p値を使用して、分布の適合を評価します。
- 業界またはアプリケーションで最も一般的に使用される分布を選択します。
- 最も控えめな結果が得られる分布を選択します。たとえば、工程能力分析を実行する場合は、異なる分布を使用して分析を実行し、最も控えめな工程能力指標が生成される分布を選択できます。詳細は、個別の分布の識別の分布の百分位数を参照し、[パーセントと百分位数]をクリックします。
- データによくあてはまる最も単純な分布を選択します。たとえば、2-パラメータと3-パラメータの分布がどちらもうまくあてはまる場合は、より単純な2-パラメータ分布を選択できます。
AD
Anderson-Darling適合度統計量(AD)は、(選択した分布に基づく)適合線と(データ点に基づく)ノンパラメトリックステップ関数の間の変動の測度です。Anderson-Darling統計量は、分布の裾のほうが重み付けが大きい二乗距離です。
解釈
Minitabでは、Anderson-Darling統計量を使用してp値を計算します。p値は、データが分布に従うという帰無仮説を棄却する証拠を測定する確率です。
一般に、Anderson-Darling統計量の値が大幅に小さくなっている場合は、データが分布により緊密に従うことを示しています。ただし、AD統計量は分布の種類が異なれば分布の仕方も異なるため、AD値どうしが近い値の場合は異なる分布間でAD値を直接比較することは避けてください。異なる分布の適合度をより良い方法で比較するには、確率プロット、p値、および工程に関する知識などの追加基準を使用してください。
P
注
3-パラメータ分布では、ワイブル分布の場合を除いて、AD検定で使用可能なp値はありません。
解釈
p値は、分布の適合度を評価するために使用します。
- P ≤ α: データは分布に従いません(H0を棄却する)
- p値が有意水準以下の場合は、帰無仮説を棄却する決定を下し、データは分布に従わないと結論付けます。
- P > α: データは分布に従わないと結論付けることはできません(H0を棄却しない)
- p値が有意水準よりも大きい場合は、帰無仮説を棄却しない決定を下します。この場合、データは分布に従わないと結論付ける十分な証拠はありません。データは分布に従うと仮定できます。
- 業界またはアプリケーションで最も一般的に使用される分布を選択します。
- 最も保守的な結果が得られる分布を選択します。 たとえば、工程能力分析を実行する場合は、異なる分布を使用して分析を実行し、最も保守的な工程能力指標が生成される分布を選択できます。詳細は、個別の分布の識別の分布の百分位数を参照し、「パーセントと百分位数」をクリックします。
- データによくあてはまる最も単純な分布を選択します。たとえば、2-パラメータと3-パラメータの分布がどちらもうまくあてはまる場合は、より単純な2-パラメータ分布を選択できます。
重要
非常に小さいか非常に大きいサンプルからの結果を解釈する場合は、注意を要します。サンプルサイズが非常に小さい場合は、適合度検定の検出力が分布からの有意な偏差を検出するのに十分ではない可能性があります。サンプルサイズが非常に大きい場合は、検定の検出力が非常に強く、現実的に有意ではない分布からの小さな偏差が検出される可能性があります。p値に加えて、確率プロットを使用して分布の適合を評価してください。
適合度検定
| 分布 | AD | p値 | 尤度比検定 p値 |
|---|---|---|---|
| 正規 | 0.754 | 0.046 | |
| Box-Cox変換 | 0.414 | 0.324 | |
| 対数正規 | 0.650 | 0.085 | |
| 3-パラメータ対数正規 | 0.341 | * | 0.017 |
| 指数 | 20.614 | <0.003 | |
| 2-パラメータ指数 | 1.684 | 0.014 | 0.000 |
| ワイブル | 1.442 | <0.010 | |
| 3-パラメータワイブル | 0.230 | >0.500 | 0.000 |
| 最小極値 | 1.656 | <0.010 | |
| 最大極値 | 0.394 | >0.250 | |
| ガンマ | 0.702 | 0.071 | |
| 3-パラメータガンマ | 0.268 | * | 0.006 |
| ロジスティック | 0.726 | 0.034 | |
| 対数ロジスティック | 0.659 | 0.050 | |
| 3-パラメータ対数ロジスティック | 0.432 | * | 0.027 |
| Johnson変換 | 0.124 | 0.986 |
これらの結果において、いくつかの分布のp値は0.05より大きくなっています。3-パラメータワイブル分布(P > 0.500)と最大極値分布(P > 0.250)のp値は最大であり、他の分布よりもサンプルデータの適合度が高くなっています。また、Box-Cox変換(P = 0.324)とJohnson変換(P = 0.986)は、正規分布に従うようにデータを変換する場合に有効です。
注
いくつかの分布の場合、Minitabには、追加パラメータを使用した場合の分布の結果も表示されます。たとえば、対数正規分布の場合は、2-パラメータと3-パラメータ両方の場合の分布バージョンの結果が表示されます。追加パラメータを使用する分布の場合は、尤度比検定p値(LRT P)を使用して、別のパラメータを追加すると分布の適合度が有意に改善されるかどうかを判断します。尤度比検定p値が0.05未満であれば、適合度が有意に改善されることを示します。詳細は、尤度比検定p値についてのセクションを参照してください。
尤度比検定p値
いくつかの分布の場合、Minitabには、追加パラメータを使用した分布の結果も表示されます。特別なパラメータを含む分布バージョンごとに、尤度比検定のp値(LRT P)が報告されます。p値は帰無仮説を棄却するための証拠を測定する確率です。個別の分布の識別での尤度比検定の場合、帰無仮説は、データは小さな(下限パラメータ)分布に従うというものです。したがって、尤度比検定p値が低いほど、追加パラメータを使用することにより分布の適合が有意に改善されるということの強力な証拠となります。
解釈
尤度比検定p値を使用して、特別なパラーメータを使用する場合としない場合のどちらが分布への適合度が有意に改善されるかを判断します。
- P ≤ α: 分布が大きい(上限パラメータ)ほど適合度が有意に高くなります。(H0を棄却する)
- p値が有意水準以下の場合は、帰無仮説を棄却し、分布の適合は追加パラメータを使用することによって有意に改善されると結論付けます。
- P > α: 大きな(上限パラメータ)分布では適合度が有意に高くなるとは結論できません(H0を棄却しない)
- p値が有意水準よりも大きい場合は、帰無仮説を棄却できません。この場合、分布の適合は追加パラメータを使用することによって有意に改善されると結論する十分な証拠はありません。
尤度比検定p値は、p値を計算するための確立された方法がない3-パラメータ分布の場合にも有効です。これらの場合には、まず対応する2-パラメータ分布のp値を調べます。次に、3-パラメータ分布の尤度比検定p値を調べて、3-パラメータ分布が2-パラメータ分布と比べて有意に良好かどうかを判断します。
これらの結果において、各分布の尤度比検定p値(3-パラメータ対数正規(0.017)、3-パラメータワイブル(0.000)、3-パラメータガンマ(0.004)、および3-パラメータ対数ロジスティック(0.027))は、これらの分布では対応する2-パラメータ分布と比べて適合度が有意に改善されることを示しています。
適合度検定
| 分布 | AD | p値 | 尤度比検定 p値 |
|---|---|---|---|
| 正規 | 0.754 | 0.046 | |
| Box-Cox変換 | 0.414 | 0.324 | |
| 対数正規 | 0.650 | 0.085 | |
| 3-パラメータ対数正規 | 0.341 | * | 0.017 |
| 指数 | 20.614 | <0.003 | |
| 2-パラメータ指数 | 1.684 | 0.014 | 0.000 |
| ワイブル | 1.442 | <0.010 | |
| 3-パラメータワイブル | 0.230 | >0.500 | 0.000 |
| 最小極値 | 1.656 | <0.010 | |
| 最大極値 | 0.394 | >0.250 | |
| ガンマ | 0.702 | 0.071 | |
| 3-パラメータガンマ | 0.268 | * | 0.006 |
| ロジスティック | 0.726 | 0.034 | |
| 対数ロジスティック | 0.659 | 0.050 | |
| 3-パラメータ対数ロジスティック | 0.432 | * | 0.027 |
| Johnson変換 | 0.124 | 0.986 |
