N
サンプル内の非欠損値の数。Nはすべての観測値の数です。
| 合計 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
解釈
Nは、サンプルサイズを評価するために使用します。
重要
非常に小さいか非常に大きいサンプルからの結果を解釈する場合は、注意を要します。サンプルサイズが非常に小さい場合は、適合度検定の検出力が分布からの有意な偏差を検出するのに十分ではない可能性があります。サンプルサイズが非常に大きい場合は、検定の検出力が非常に強く、現実的に有意ではない分布からの小さな偏差が検出される可能性があります。p値に加えて、確率プロットを使用して分布の適合を評価してください。
N*
サンプルにおける欠損値の数。N*は、欠損値記号*を含むワークシート内のセルの計数です。
| 合計 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
平均
平均値は、データの平均として計算され、すべての観測値の和を観測値の数で割って求められます。
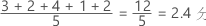
解釈
平均値を使用して、データの中心を表す単一の値でサンプルを記述します。多くの統計的分析では、標準的な参照点として平均値を使用します。
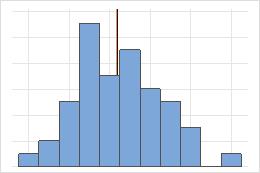
対称分布における平均値と中央値
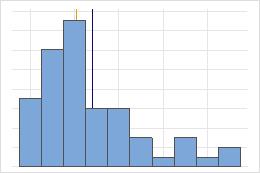
非対象分布における平均値と中央値
対称分布の場合、平均値(青の線)と中央値(オレンジの線)はほとんど同じになります。したがって、両方の線が重なり、相互に識別することはできません。非対称分布の場合は、データが右方向に歪み、平均値が中央値よりも大きくなります。
標準偏差
標準偏差(StDev)は、散布度、つまり平均値周辺でのデータの広がり方を表す最も一般的な測度です。記号σ(シグマ)は、母集団の標準偏差を表す場合によく使用されるのに対し、sはサンプルの標準偏差を表すために使用されます。
解釈
標準偏差を使用して、平均値からのデータの分散の状態を判断します。サンプルの標準偏差が大きいほど、平均周辺のより広い範囲にデータが分散していることを示します。
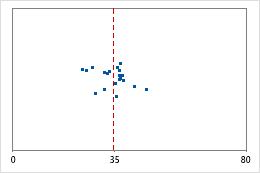
病院1

病院2
退院時間
管理者が、2つの病院の救急部門で処置を受けた患者の退院時間を追跡するとします。平均退院時間はほぼ同じ(35分)ですが、標準偏差には有意差があります。病院1の標準偏差はおよそ6です。平均すると、患者の退院時間は平均(点線)から約6分離れています。病院2の標準偏差はおよそ20です。平均すると、患者の退院時間は平均(点線)から約20分離れるています。
中央値
中央値はデータセットの中間点です。この中間点の値は、観測値の半分がその値より上にあり、観測値の半分がその値より下にあるという点です。中央値は、観測値に順位付けして、順位付けされた順序での順位が[N + 1] / 2の観測値を検出することによって算定されます。観測値の数が偶数の場合、中央値は、順序付けされた順位がN / 2と[N / 2] + 1の観測値間の値です。

この順序付けされたデータの場合、中央値は13です。つまり、半数の値が13以下で、半数の値が13以上になっています。
解釈

対称分布における平均値と中央値

非対象分布における平均値と中央値
対称分布の場合、平均値(青の線)と中央値(オレンジの線)はほとんど同じになります。したがって、両方の線が重なり、相互に識別することはできません。非対称分布の場合は、データが右方向に歪み、平均値が中央値よりも大きくなります。
最小値
最小データ値。
これらのデータでの最小値は7です。
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
解釈
最小値を使用して、可能性のある外れ値を特定します。値が異常に低い場合は、データ入力ミスや測定誤差などの考えられる要因を調査します。
データの広がりを評価するための最も簡単な方法の1つは、最小値と最大値を比較してその範囲を判断することです。範囲は、データセットの最大値と最小値の差です。データの広がりを評価する場合は、標準偏差などのその他の測定値も考慮します。
最大値
最大データ値。
これらのデータでの最大値は19です。
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
解釈
最大値を使用して、可能性のある外れ値を特定します。値が異常に高い場合は、データ入力ミスや測定誤差などの考えられる要因を調査します。
データの広がりを評価するための最も簡単な方法の1つは、最小値と最大値を比較してその範囲を判断することです。範囲は、データセットの最大値と最小値の差です。データの広がりを評価する場合は、標準偏差などのその他の測定値も考慮します。
歪度
歪度とは、データの非対称性の度合いを示す度数です。
解釈
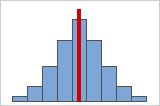
図A: 対称な正規分布データ
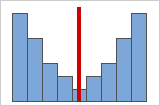
図B: 対称な非正規分布データ
対称な(歪みのない)分布
データは、対称性が高くなるほど、歪度の値が0に近付きます。図Aに、定義によりその歪度が比較的小さな値を示している正規分散データを示します。正規データのヒストグラムの中間にある線は、2つの側が相互にミラーイメージになっていることを示しています。ただし、それ自体に歪度が発生しなくても、正規性を意味するわけではありません。図Bに、2つの側が相互にミラーイメージになっていてもデータは正規分布していない分布を示します。
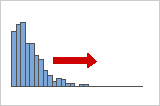
正(右)方向に歪んだ分布
正方向に歪んだデータは、分布の「裾」が右側にずれるため、右方向に歪んだデータとも呼ばれます。正方向に歪んだデータの歪度の値は0より大きくなります。給与データは正方向に歪むことが多くありますが、これは、社内の多くの従業員が受け取る給与が相対的に少額であるのに対し、さらに少数の人が非常に高額の給与を受け取るからです。
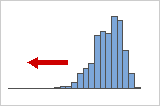
負(左)方向に歪んだ分布
負方向に歪んだデータは、分布の「裾」が左側にずれるため、多くの場合に左方向に歪んだデータと呼ばれます。負方向に歪んだデータの歪度の値は0未満になります。故障率データは、多くの場合に負方向に歪んだデータとなります。たとえば、すぐに切れる電球の数は非常に少なく、ほとんどの電球は長期間に渡って焼き切れない場合です。
尖度
尖度は、分布の裾の正規分布からの逸脱の程度を示します。
解釈
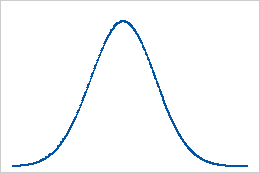
ベースライン:尖度の値が0
正規分布に完全に従うデータの尖度値は0です。正規分布したデータは、尖度のベースラインとなります。0から著しく逸脱している尖度は、データが正規に分布していないことを示す可能性があります。
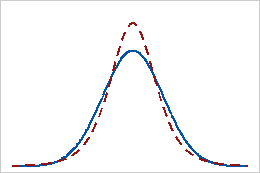
尖度の値が正
尖度の値が正の分布は、その分布に正規分布と比べて重い裾があることを示します。たとえば、t分布に従うデータの尖度は正の値になります。実線は正規分布を示し、点線は尖度の値が正のt分布を示しています。
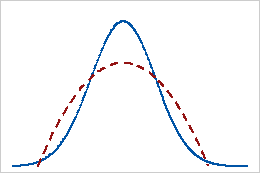
尖度の値が負
尖度の値が負の分布は、その分布に正規分布と比べて軽い裾があることを示します。たとえば、最初の形状パラメータと2番目の形状パラメータが2であるベータ分布に従うデータの尖度は負の値になります。実線は正規分布を示し、点線は尖度の値が負のベータ分布を示しています。
