個別の分布の識別の例

結果を解釈する

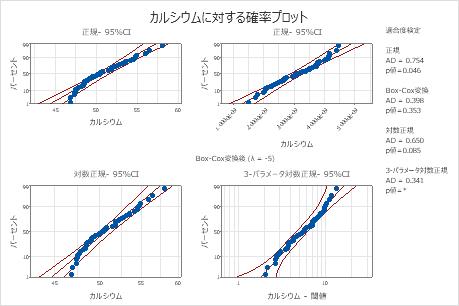
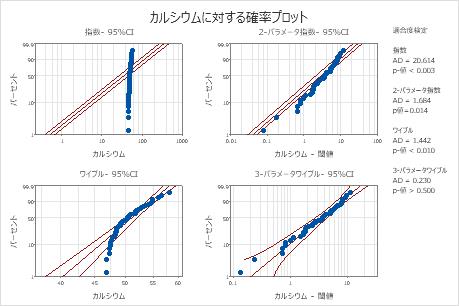
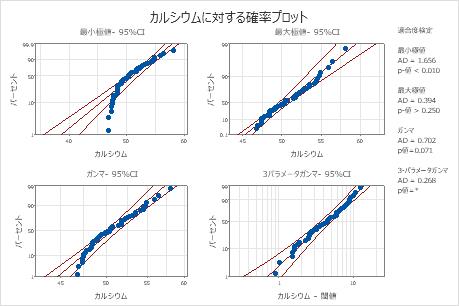
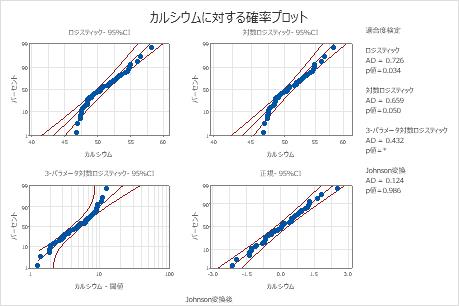
Minitabには、各分布と変換ごとに確率プロットとp値が表示されます。分布がデータによくあてはまる場合（または変換が有効な場合）、プロット上の点は信頼限界内の直線に従い、p値はα水準より大きくなります。多くの場合、α水準として0.05が使用されます。尤度比検定（LRT）のp値は、追加パラメータを分布に追加することにより適合度が有意に改善されるかどうかを示します。尤度比検定p値が0.05未満であれば、適合度が有意に改善されることを示します。　

これらのデータの場合、3-パラメータワイブル分布（p > 0.500）と最大極値分布（p > 0.250）がデータにうまくあてはまります。3番目のパラメータを追加すると、対数正規分布（LRT P = 0.017）、ワイブル分布（LRT P = 0.000）、ガンマ分布（LRT P ＝ 0.006）、および対数ロジスティック分布（LRT P = 0.027）の適合度が有意に改善されます。

Box-Cox変換（p = 0.324）とJohnson変換（p = 0.986）は、これらのデータで有効です。変換後、正規分布は変換された値によくあてはまります。

記述統計量

N	欠損値	平均	標準偏差	中央値	最小	最大	歪度	尖度
50	0	50.782	2.76477	50.4	46.8	58.1	0.644923	-0.287071

Box-Cox変換: λ = -4

Johnson変換関数:

0.804604 + 0.893699×Ln ((X - 46.2931)/(59.8636 - X))

適合度検定

分布	AD	p値	尤度比検定 p値
正規	0.754	0.046
Box-Cox変換	0.414	0.324
対数正規	0.650	0.085
3-パラメータ対数正規	0.341	*	0.017
指数	20.614	<0.003
2-パラメータ指数	1.684	0.014	0.000
ワイブル	1.442	<0.010
3-パラメータワイブル	0.230	>0.500	0.000
最小極値	1.656	<0.010
最大極値	0.394	>0.250
ガンマ	0.702	0.071
3-パラメータガンマ	0.268	*	0.006
ロジスティック	0.726	0.034
対数ロジスティック	0.659	0.050
3-パラメータ対数ロジスティック	0.432	*	0.027
Johnson変換	0.124	0.986

分布パラメータの最尤推定値

分布	位置	形状	尺度	閾値
正規*	50.78200		2.76477
Box-Cox変換*	0.00000		0.00000
対数正規*	3.92612		0.05368
3-パラメータ対数正規	1.69295		0.46849	44.74011
指数			50.78200
2-パラメータ指数			4.06326	46.71873
ワイブル		17.82470	52.13681
3-パラメータワイブル		1.47605	4.53647	46.66579
最小極値	52.22257		2.95894
最大極値	49.50370		2.16992
ガンマ		351.04421	0.14466
3-パラメータガンマ		2.99218	1.63698	45.88376
ロジスティック	50.57182		1.59483
対数ロジスティック	3.92259		0.03121
3-パラメータ対数ロジスティック	1.54860		0.32763	45.46180
Johnson変換*	0.02897		0.97293