このトピックの内容
自由度
SS(平方和)ごとの自由度(DF)。一般に、自由度では、各SSを計算するために使用できる情報の量を測定します。
平方和(SS)
平方和(SS)は平方距離の和であり、異なるソースから得られたばらつきの測度です。平方和(SS)の合計は、全体平均のデータのばらつきの量を示しています。SS演算子は、演算子ごとの平均測定値と全体平均のばらつきの量を示しています。
SS合計 = SS測定者 + SS部品(測定者) + SS繰り返し性
平均平方
平均平方(MS)は異なるソースから得られるデータのばらつきです。MSは、異なるソースに異なる数値の水準または発生し得る値があるという事実を説明します。
変動性の各要因でMS = SS/DF
F
測定者または部品(測定者)の効果が測定に有意に影響するかどうかの判定に使用される統計量。
F統計量が大きくなるほど、因子は応答変数または測定変量の変動により有意に寄与します。
P
p値は、サンプルから計算される値と少なくとも同程度に極端な検定統計量(F統計量など)を得る確率です。
解釈
分散分析表にp値を使用して、平均測定値が著しく異なるかどうかを判断します。
p値が低い場合、すべての測定者または部品(測定者)の平均が同じであるという仮定が真でない可能性が高いことを示しています。
- p値 ≤ α:少なくとも1つの平均に有意な差がある
- p値が有意水準以下の場合、帰無仮説を棄却し、少なくとも1つの平均値がその他の平均値と著しく異なっていることを結論付けます。たとえば、少なくとも1人の測定者は異なる測定をします。
- p値 > α:平均には有意な差がない
- p値が有意水準より大きい場合、母平均が異なると結論付ける十分な根拠はないので、帰無仮説の棄却は失敗します。たとえば、測定者が異なる測定をするとは結論付けられません。
分散成分
分散成分とは、分散分析表の各要因の推定された分散成分です。
解釈
分散成分を使用して、測定誤差の各要因による変動を評価します。
合格測定システムでは、最も大きい分散成分は部品間変動です。繰り返し性と再現性が大きな変動量に寄与している場合、問題のソースを調査して修正する必要があります。
寄与度(分散成分)
%寄与度は各分散成分と分散全体の割合です。%寄与度は、全変動によって分割されたソースごとの分散成分として計算され、100を掛けて百分率として表現します。
解釈
測定誤差の各要因による変動を評価するには、寄与度を使用します。
合格測定システムでは、最も大きい分散成分は部品間変動です。繰り返し性と再現性が大きな変動量に寄与している場合、問題のソースを調査して修正する必要があります。
標準偏差(SD)
標準偏差(SD)は、変動のソースごとの標準偏差です。標準偏差は、そのソースの分散成分の平方根と等しくなります。
標準偏差は、部品測定値および公差と同じ単位を使用するため、変動の測定値として便利です。
基準変動(6 * SD)
基準変動は、6または基準変動で指定した乗数を掛けた変動のソースごとの標準偏差として計算します。
通常、工程変動は6sとして定義されます。ここでsは、母集団の標準偏差(σまたはシグマと表されます)の推定値としての標準偏差です。データが正規分布の場合、約99.73%のデータが平均から標準偏差の6倍以内の範囲にあります。異なる割合のデータを定義するには、標準偏差に別の乗数を使用します。たとえば、99%のデータの範囲を知るには、乗数にデフォルトの6ではなく5.15を使用します。
%基準変動(%SV)
%基準変動は、全変動で割って100を掛けた変動のソースごとの基準変動として計算します。
%基準変動は、そのソースの計算された分散成分(VarComp)の平方根です。このため、分散成分の%寄与度の値を合計すると100になりますが、%基準変動は100になりません。
解釈
測定システムの変動を全変動と比較する際には、%基準変動を使用します。部品間変動の低減など、工程改善を評価するために測定システムを使用する場合は、%基準変動によって測定の正確性をより的確に推定できます。部品を規格と比較して評価するために測定システムの工程能力を評価する場合は、%公差が適切な基準です。
%公差(SV/Toler)
%公差は、各要因の基準変動を工程変動で割り、100を掛けて計算されます。
公差を入力することで、Minitabは%公差を計算し、測定システムの変動を規格と比較します。
解釈
%公差を使用して、部品を規格と比較して評価します。部品間変動の低減など、工程改善のために測定システムを使用する場合は、%基準変動が適切な基準です。
%工程変動(SV/Proc)
工程変動を推定するために過去の標準偏差を入力したものの分析内の部品を使用する場合、Minitabでは%工程変動を計算します。%工程変動は測定システムの変動と過去の工程変動を比較します。ソースごとの基準変動として計算される%工程変動は、過去の工程変動で割って100を掛けた数になります。デフォルトでは、工程変動は過去の標準偏差を6倍にしたものと等しくなります。
工程変動を推定するために過去の標準偏差を指定する場合、%工程変動は%基準変動と同じため%工程変動は表示されません。
95%信頼区間
95%信頼区間は、各測定誤差基準の真の値が含まれている可能性のある値の範囲です。
Minitabでは、分散成分、分散成分の寄与度、標準偏差、基準変動、%基準変動、%公差、および知覚区分数に対して信頼区間を使用できます。
解釈
データのサンプルはランダムであるため、2つのゲージ分析の信頼区間が同一である可能性は低くなります。ただし、分析を何度も繰り返した場合、その結果の信頼区間のうち特定の割合には未知の真の測定誤差が含まれています。このようなパラメータを含む信頼区間の割合(%)を区間の信頼水準と言います。
たとえば、信頼水準が95%の場合、信頼区間に真の値が含まれていることが95%信頼できます。信頼区間は、結果の実質的な有意性を評価するのに役立ちます。状況に応じた専門知識を利用して、信頼区間に実質的に有意な値が含まれているかどうかを判断します。信頼区間が広すぎて有用でない場合は、サンプルサイズを増やすことを検討します。
繰り返し性の分散成分が0.044727で、対応する95%信頼区間が(0.035, 0.060)であるとします。データから計算された繰り返し性の変動の推定値は0.044727です。繰り返し性の真の変動は0.035~0.060に含まれることが95%信頼できます。
知覚区分数
知覚区分数は、測定した特性の差を検出する測定システムの能力を表すために、ゲージのR&R分析で使用される基準です。知覚区分数は、選択したサンプルで定義される製品変動の範囲内にある重複していない信頼区間の数を表します。また、知覚区分数は、使用中の測定システムが工程データ内で識別できるグループ数を表します。
解釈
Automobile Industry Action Group(AIAG)が発行した測定システム分析マニュアル1では、5つ以上のカテゴリがあれば、許容できる測定システムであるとされています。知覚区分数が5未満の場合、測定システムの分解能が十分でない可能性があります。
通常、知覚区分数が2未満の測定システムは、部品の区別ができないため、工程管理に使用できないと見なされています。知覚区分数が2の場合、部品を「高」と「低」というような2グループにのみ分けることができます。知覚区分数が3なら、データを「高」、「中」、「低」というような3グループに分けることができます。
詳細は、「知覚区分数の使用」を参照してください。
誤判別確率
1つ以上の規格限界を指定すると、製品の誤判別確率を計算できます。ゲージは変動するため、部品を測定した値は、部品の真の値と常に一致するわけではありません。測定値と実際の値の相違は、部品の誤判別につながる可能性があります。
- 同時確率
- 部品を許容できるかどうかについて事前の情報がない場合は、同時確率を使用します。たとえば、ラインからサンプル抽出を行うときに各部品が良好であるか不良であるかが分からない場合です。起こり得る誤判別は2つあります。
- 不良品を合格と判別する確率
- 良品を不合格と判別する確率
- 条件付き確率
- 部品を許容できるかどうかについて事前の情報がある場合、条件付き確率を使います。たとえば、再加工対象の製品群からサンプル抽出を行ったり、良品として出荷する予定の製品群からサンプル抽出を行う場合です。起こり得る誤判別は2つあります。
- 再加工が必要な不良品群からサンプル抽出された部品を合格と判別する確率(誤った合格)
- 出荷予定の良品群からサンプル抽出された部品を不合格と判別する確率(誤った不合格)
解釈
同時確率
| 説明 | 確率 |
|---|---|
| ランダムに選んだ部品が不良品でも合格 | 0.037 |
| ランダムに選んだ部品が良品でも不合格 | 0.055 |
条件付き確率
| 説明 | 確率 |
|---|---|
| 不良品グループ内の部品が合格 | 0.151 |
| 良品グループ内の部品が不合格 | 0.073 |
不良品を合格と判別する同時確率は0.037です。良品を不合格と判別する同時確率は0.055です。
実際は規格外の部品を再検査で合格と判別する誤った合格の条件付き確率は0.151です。実際は規格内の部品を再検査で不合格と判別する誤った不合格の条件付き確率は0.073です。
VDA 5
注
VDA 5 は Web アプリ専用です。
注
この解析では、uEVR、uRE、およびuEVO間の最大不確かさを使用して、測定プロセスの変動を計算します。他の 2 つの統計の % of Total は、それらの統計が合計に寄与しないため、欠落しています。
- キャリブレーション(uCAL)
- キャリブレーション(uCAL)は、参照標準の校正による測定値の不確かさです。この統計量は、分析への入力です。通常、この値は校正証明書から取得されます。
- 参照時の再現性(uEVR)
- 基準での再現性(uEVR)は、同じオペレーターが同じデバイスを使用して基準部品を繰り返し測定することによる不確かさです。この統計量は、分析への入力です。通常、この値はタイプIゲージ研究から取得されます。
- 分解能(uRE)
- 分解能(uRE)は、ゲージの分解能による不確かさです。分析では、ゲージの分解能が分析への入力である場合に、この統計量が計算されます。
- 測定対象物の再現性(uEVO)
- 測定対象物の再現性 (uEVO) は、Gage R&R 研究における再現性による不確実性です。再現性とは、同じオペレーターが同じ部品を複数回測定した場合の測定のばらつきです。
- 偏り(uBI)
- 偏り (uBI) は、既知の基準測定値と研究の測定値の平均との差による測定値の不確実性です。この統計量は、分析への入力です。通常、この値は、参照部分が測定範囲内にあるバイアス研究から取得されます。
- 線形性(uLIN)
- 線形性(uLIN)は、直線性からの測定の不確かさです。直線性は、参照部品の値と、部品の値の変化に伴うバイアスの変化から生じる平均測定値との差です。この統計量は、分析への入力です。通常、この値は、参照部品が測定範囲内にある線形性スタディから取得されます。
- その他の要因 (uREST)
- その他の要因 (uREST) は、1 つ以上の追加要因による測定の不確実性です。解析の仕様に 1 つの追加要素がある場合、この不確かさは解析への入力となります。分析の仕様に複数の因子がある場合、この不確実性は値を結合します。たとえば、データ収集がより高い温度で測定値の差が大きくなる場合、温度による不確実性を説明するために、他の要因の仕様を使用します。
- オペレーター(uAV)
- オペレーター (uAV) は、Gage R&R 研究における再現性による測定の不確実性です。再現性とは、異なるオペレーターが同じ部品を測定した場合の測定のばらつきです。
- 測定プロセス(uMP)
- 測定プロセス(uMP)は、すべての不確かさコンポーネントを組み合わせて、測定プロセスからの総不確かさを推定します。
- 合計の%
- 不確実性の原因ごとに、分析では、その原因から生じるuMPの割合が表示されます。パーセンテージを使用して、さまざまなソースからの不確実性の量を比較します。
- 許容値の %(%QMP)
- 公差%(%QMP)は、測定プロセスの不確かさと試験の変動を組み合わせ、その値をプロセス公差と比較します。%QMP は、測定プロセスが満足のいくものであるかどうかを判断する一般的な方法です。一部のアプリケーションでは、30%以下の値は、測定プロセスが満足のいくものであることを示します。
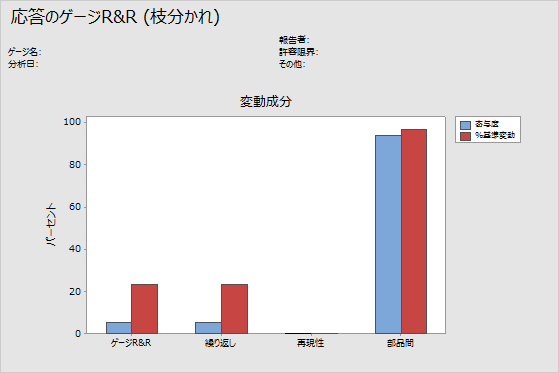
変動成分グラフ
変動成分管理図は、ゲージのR&R分析の結果のグラフ要約です。
- 合計ゲージR&R:繰り返し性と再現性の分散成分の和。
- 繰り返し性:同じ測定者が同じバッチから部品を測定するときの測定値の変動。
- 再現性:異なる測定者が部品を測定したときの測定値の変動。
- 部品間:異なる部品によって生じる測定値の変動。
解釈
- %寄与度
- %寄与度は、各分散成分と変動全体の割合です。%寄与度は、全変動で割って100を掛けたソースごとに分散成分として計算します。
- %基準変動
- %基準変動は各ソースと変動全体の割合です。%基準変動は、全変動で割って100を掛けたソースごとの基準変動として計算します。
- %公差
- %公差は測定システムと規格を比較します。%公差は、工程公差で割って100を掛けたソースごとの基準変動として計算します。
- %工程変動
- %工程変動は測定システムの分散と分散変動を比較します。%工程変動は、過去の工程変動で割って100を掛けたソースごとの基準変動として計算します。
合格測定システムでは、最大の分散成分が部品間変動です。
R管理図
R管理図は、測定者の一貫性を示す範囲の管理図です。
- プロットされた点
- 測定者ごとの、部品ごとの測定値の最大値と最小値の差。R管理図では、測定者ごとにデータ点がプロットされているので、各測定者の一貫性を確認できます。
- 中心線(Rbar)
- 工程の全体平均(つまり、すべてのサンプル範囲の平均)。
- 管理限界(LCLとUCL)
- サンプル範囲の期待変動量。管理限界を計算するために、Minitabではサンプル内の変動が使用されます。
注
各測定者が各部品を9回以上測定する場合、R管理図のかわりにSチャートが表示されます。
解釈
平均範囲が小さい場合、測定システムの分散が低いことを示しています。上側臨界境界(UCL)より高い点は、測定者の部品測定に一貫性がないことを示します。UCLの計算に、各測定者による部品ごとの測定値数と部品間の変動が含まれています。測定者の部品測定に一貫性がある場合、基準変動を基準にして最大と最小の測定値の範囲は小さくなり、データ点は臨界内にあります。
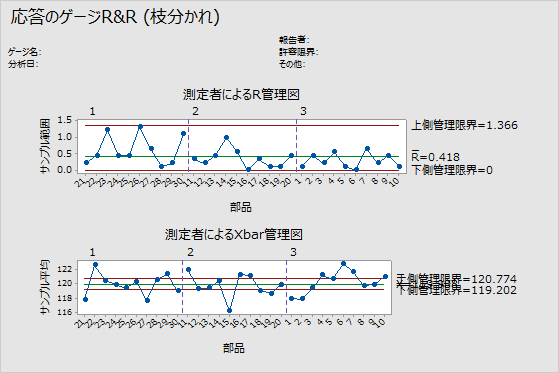
Xbar管理図
Xbar管理図は、部品間の変動を繰り返し性と比較します。
- プロットされた点
- 各測定者がプロットした部品ごとの平均測定値。
- 中心線(Xbar)
- すべての測定者によるすべての部品の測定値の全体平均。
- 管理限界(LCLとUCL)
- 臨界距離は繰り返し性の測定値と平均ごとの測定値の数に基づいています。
解釈
ゲージR&R分析で選択されている部品は、可能性のある部品の範囲全体を表す必要があります。したがって、このグラフは、部品の平均間の分散が、繰り返し性の分散のみから予測される分散よりも大きくなることを示す必要があります。
グラフに、低い分散を持つ測定システムがあることを示す臨界の範囲外の点が多く、臨界距離が狭いのが理想的です。

部品(測定者)別グラフ
部品別(測定者別)の図には、分析で計算され、部品ごとに並べられたすべての測定値が表示されます。このグラフには、因子水準間の差が表示されます。ゲージR&R分析は通常、部品別、測定者別に測定値を並べます。ただし、拡張ゲージR&R分析を使用すれば、他の因子もグラフ化できます。
グラフでは、ドットは測定値を表し、マルバツ記号は平均を表します。結線は因子水準ごとの平均測定値をつなげます。
注
水準あたりの観測数が9を超えると、個別値プロットの代わりに、箱ひげ図が表示されます。
解釈
個々の部品ごとの複数の測定値が可能な限り最小に変動する(1つの部品のドットが近似する)場合、測定システムの分散が低いことを示します。また、部品の平均測定値部品は、工程の範囲全体を表していることを十分に示すほど変動します。
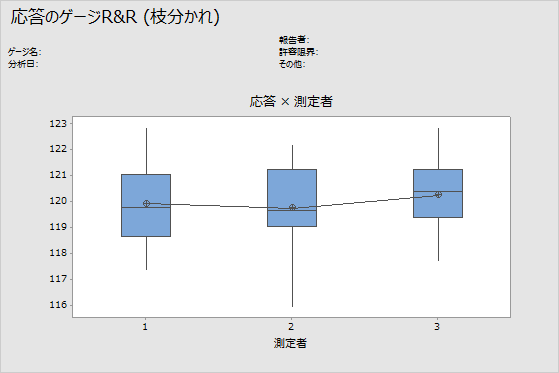
測定者別グラフ
測定者別の図には、分析内で計算され、測定者別に並べられたすべての測定値が表示されます。このグラフには因子水準間の差が示されます。ゲージR&R分析は通常、部品別、測定者別に測定値が並べられます。ただし、拡張ゲージR&R分析を使用すれば、他の因子もグラフ化できます。
注
測定者あたりの観測数が9より多い場合、個別値プロットの代わりに、箱ひげ図が表示されます。
解釈
全測定者にわたるまっすぐな水平線は、測定者ごとの平均測定値が似ていることを示しています。測定値が等しい量で測定者ごとに変化することが理想的です。