あるエンジニアが、セラミック部品の衝撃強度を監視したいと考えています。技師は、工程変動の期待範囲を表す30個の成分を無作為に選択します。各コンポーネントは、テストに適したサイズのサンプルを2つ生成するのに十分な大きさです。エンジニアは、コンポーネントからサンプルを準備し、同じコンポーネントからのサンプルに同じ部品番号を割り当てます。測定者は、測定する3人の測定者それぞれについて、10個の部品をランダムに選択します。3人のオペレーターが各サンプルの強度を測定し、部品ごとに2サンプル、合計60回の測定を行います。
測定者内で測定値が枝分かれしているため、エンジニアは枝分かれゲージR&R分析を実行し、測定システムが原因で発生している可能性のある測定値の変動を評価します。
- 標本データを開く、 セラミック部品.MTW.
- を選択します。
- 部品番号またはバッチ番号に部品を入力します。
- 測定者に測定者を入力します。
- 測定データに応答を入力します。
- OKをクリックします。
結果を解釈する
分散分析表で、測定者のp値は0.773です。p値が大きいため、帰無仮説を棄却できず、平均強度測定は、測定を行う測定者におそらく依存しないと結論付けます。ただし、部品(測定者)のp値は0.000で、0.05より小さくなっています。各測定者内で枝分かれしている異なる部品間の平均測定値には有意な差があります。
測定システムの変動を全変動と比較する際には、%基準変動を使用します。合計ゲージR&Rは基準変動の23.71%で、部品間変動は97.15%です。合計ゲージR&R変動は用途によっては許容できる場合があります。詳細は、測定システムは許容範囲内かを参照してください。
また、この測定システムの知覚区分数は5です。これの結果は、測定システムが部品を区別できることを表しています。AIAGの基準では、値が5以上のときに適切な測定システムとみなされます。詳細は、ゲージR&R分析における異なるカテゴリの数の使用を参照してください。
グラフから、測定システムに関する次の情報も得られます。
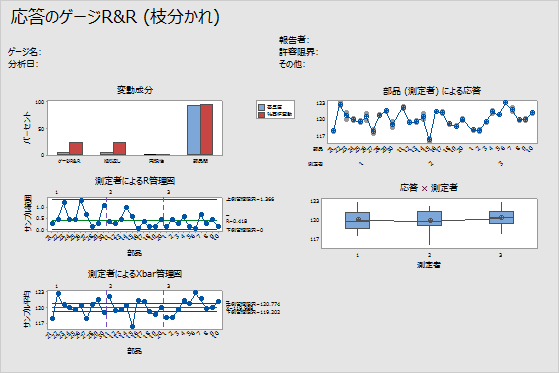
- 変動成分グラフでは、ほとんどの変動は部品間変動によって説明されます。
- 測定者別R管理図では、すべてのデータは正常に管理されており、これは、3人の測定者の測定に一貫性があることを示しています。
- 測定者別Xbar管理図では、いくつかの点が管理限界を超えています。したがって、変動の大部分が、部品間の差によることがわかります。
- 部品別グラフは、部品間の差が大きいことを示しています。
- 測定者別グラフでは、各測定者の測定値の変動量がほぼ同じです。また、部品平均の変動量は小さくなっています。いくらかの変動は常に存在しますが、データは、測定者が部品を同様に測定していることを示しています。
ゲージR&R-枝分かれ型分散分析
応答のゲージR&R (枝分かれ)
要因 自由度 平方和 平均平方 F値 p値
測定者 2 2.618 1.30922 0.2594 0.773
部品 (測定者) 27 136.285 5.04758 34.5709 0.000
繰り返し性 30 4.380 0.14601
合計 59 143.283
分散成分
（分散成
分の）寄
要因 分散成分 与度
合計ゲージR&R 0.14601 5.62
繰り返し性 0.14601 5.62
再現性 0.00000 0.00
部品間 2.45079 94.38
全変動 2.59679 100.00
ゲージ評価
標準偏 基準変動 %基準変
要因 差 (SD) (6×SD) 動(%SV)
合計ゲージR&R 0.38211 2.29265 23.71
繰り返し性 0.38211 2.29265 23.71
再現性 0.00000 0.00000 0.00
部品間 1.56550 9.39300 97.15
全変動 1.61146 9.66874 100.00
知覚区分数 = 5
応答のゲージR&R (枝分かれ)
